1
1998
... 对手建模不仅关注竞争场景下的敌方智能体建模,而且还考虑合作场景下的友方建模,因此,有些文献又称其为建模其他智能体.从理论上讲,完全理性的智能体能够做出当前条件下的最优策略,实现收益的最大化.然而,现实情况下的智能体通常只具有有限程度理性[1],决策受到情绪、偏好等影响,往往以“满意”作为收益标准.此外,基于规则的智能体,如产生式规则、启发式算法等[2-4],遵循预置规则机制,行为模式僵硬、易于预测、理性程度不足,对手建模技术使智能体能够快速适应对手的行为方式并且在对抗中利用其弱点获取更高收益,或在合作中使团队获得更大回报.现有的对手建模方法如策略重构、类型推理、意图识别、递归推理等方法[5],具有模型可解释、认知推理层次深的特性.然而,要进一步应用于贴近现实的问题场景仍然存在动态环境适应性弱、特征选取复杂、状态空间表示能力不足、方法在规模上的可扩展性不强等诸多缺陷. ...
Agent-based Evolutionary Approach for Interpretable Rule-based Knowledge Extraction
1
35
... 对手建模不仅关注竞争场景下的敌方智能体建模,而且还考虑合作场景下的友方建模,因此,有些文献又称其为建模其他智能体.从理论上讲,完全理性的智能体能够做出当前条件下的最优策略,实现收益的最大化.然而,现实情况下的智能体通常只具有有限程度理性[1],决策受到情绪、偏好等影响,往往以“满意”作为收益标准.此外,基于规则的智能体,如产生式规则、启发式算法等[2-4],遵循预置规则机制,行为模式僵硬、易于预测、理性程度不足,对手建模技术使智能体能够快速适应对手的行为方式并且在对抗中利用其弱点获取更高收益,或在合作中使团队获得更大回报.现有的对手建模方法如策略重构、类型推理、意图识别、递归推理等方法[5],具有模型可解释、认知推理层次深的特性.然而,要进一步应用于贴近现实的问题场景仍然存在动态环境适应性弱、特征选取复杂、状态空间表示能力不足、方法在规模上的可扩展性不强等诸多缺陷. ...
Multi-Objective Multi-Agent Planning for Jointly Discovering and Tracking Mobile Objects
0
2020
PRIMAL: Pathfinding via Reinforcement and Imitation Multi-Agent Learning
1
2019
... 对手建模不仅关注竞争场景下的敌方智能体建模,而且还考虑合作场景下的友方建模,因此,有些文献又称其为建模其他智能体.从理论上讲,完全理性的智能体能够做出当前条件下的最优策略,实现收益的最大化.然而,现实情况下的智能体通常只具有有限程度理性[1],决策受到情绪、偏好等影响,往往以“满意”作为收益标准.此外,基于规则的智能体,如产生式规则、启发式算法等[2-4],遵循预置规则机制,行为模式僵硬、易于预测、理性程度不足,对手建模技术使智能体能够快速适应对手的行为方式并且在对抗中利用其弱点获取更高收益,或在合作中使团队获得更大回报.现有的对手建模方法如策略重构、类型推理、意图识别、递归推理等方法[5],具有模型可解释、认知推理层次深的特性.然而,要进一步应用于贴近现实的问题场景仍然存在动态环境适应性弱、特征选取复杂、状态空间表示能力不足、方法在规模上的可扩展性不强等诸多缺陷. ...
Autonomous Agents Modelling other Agents: A Comprehensive Survey and Open Problems
2
2017
... 对手建模不仅关注竞争场景下的敌方智能体建模,而且还考虑合作场景下的友方建模,因此,有些文献又称其为建模其他智能体.从理论上讲,完全理性的智能体能够做出当前条件下的最优策略,实现收益的最大化.然而,现实情况下的智能体通常只具有有限程度理性[1],决策受到情绪、偏好等影响,往往以“满意”作为收益标准.此外,基于规则的智能体,如产生式规则、启发式算法等[2-4],遵循预置规则机制,行为模式僵硬、易于预测、理性程度不足,对手建模技术使智能体能够快速适应对手的行为方式并且在对抗中利用其弱点获取更高收益,或在合作中使团队获得更大回报.现有的对手建模方法如策略重构、类型推理、意图识别、递归推理等方法[5],具有模型可解释、认知推理层次深的特性.然而,要进一步应用于贴近现实的问题场景仍然存在动态环境适应性弱、特征选取复杂、状态空间表示能力不足、方法在规模上的可扩展性不强等诸多缺陷. ...
... 根据文献[5]中的定义,对手建模是一种在无法观察到其他智能体内部状态的情况下,自身智能体以观测和先验知识为输入,通过交互、观测、推理等过程捕获无法直接感知的隐藏信息,将其他一个或多个智能体的类别、目标、动作等预测信息和意图、计划、策略等认知信息作为输出的建模方法,其核心是帮助建模者利用对手策略或根据对手隐藏的信息制定更好的响应策略. ...
Human-level Control through Deep Reinforcement Learning
2
2019
... 针对以上不足,研究者们将以深度Q网络(deep Q network, DQN)[6]为代表的深度强化学习算法(deep reinforcement learning, DRL)引入到对手建模领域.其中,强化学习是智能体学习如何与环境交互,达到最大化价值和最优策略的自主决策算法.深度学习则能够从高维感知数据中提取抽象特征,对复杂的价值函数和策略函数具有很强的拟合能力.DRL有机地结合了深度学习与强化学习,前者能够增强感知与表达能力,后者提供最优决策能力,使基于DRL的对手建模(DRL-OM)技术对复杂环境中其他智能体具有更好的认知能力,目前已在德州扑克[7-8]、星际争霸II[9]等多智能体问题场景取得优异的表现. ...
... Deep reinforcement learning algorithms in OM
Table 1| 分类 | 算法 | 优点 | 不足 |
|---|
| 值函数近似 | DQN[6] | 经验复用、离轨策略机制 | 无法用于高维、连续空间 |
| DRQN[33] | 采用LSTM代替全连接层 | 完全可观测下表现不如DQN |
| 策略梯度 | DDPG[34] | 确定性策略、Actor-Critic框架 | 无法处理离散问题、难以确定更新步长 |
| A3C[35] | 多线程学习、异步更新参数 | 更新策略方差较大 |
| PPO[37] | 有裁剪的自适应超参数KL散度 | 对差异性较大样本敏感 |
2 基于DRL的显式对手建模按照对手的理性程度和建模机理,基于DRL的显式对手建模的主要方法可以分为博弈均衡策略建模方法和递归推理建模方法.博弈均衡策略方法主张对手的绝对理性,采用博弈论的均衡原理建模,递归推理方法强调了智能体具备有限理性,从认知心理学的人类理性研究中获取灵感. ...
AlphaHoldem: High-Performance Artificial Intelligence for Heads-Up No-Limit Texas Hold'em from End-to-End Reinforcement Learning
1
2022
... 针对以上不足,研究者们将以深度Q网络(deep Q network, DQN)[6]为代表的深度强化学习算法(deep reinforcement learning, DRL)引入到对手建模领域.其中,强化学习是智能体学习如何与环境交互,达到最大化价值和最优策略的自主决策算法.深度学习则能够从高维感知数据中提取抽象特征,对复杂的价值函数和策略函数具有很强的拟合能力.DRL有机地结合了深度学习与强化学习,前者能够增强感知与表达能力,后者提供最优决策能力,使基于DRL的对手建模(DRL-OM)技术对复杂环境中其他智能体具有更好的认知能力,目前已在德州扑克[7-8]、星际争霸II[9]等多智能体问题场景取得优异的表现. ...
一种针对德州扑克AI的对手建模与策略集成框架
2
2022
... 针对以上不足,研究者们将以深度Q网络(deep Q network, DQN)[6]为代表的深度强化学习算法(deep reinforcement learning, DRL)引入到对手建模领域.其中,强化学习是智能体学习如何与环境交互,达到最大化价值和最优策略的自主决策算法.深度学习则能够从高维感知数据中提取抽象特征,对复杂的价值函数和策略函数具有很强的拟合能力.DRL有机地结合了深度学习与强化学习,前者能够增强感知与表达能力,后者提供最优决策能力,使基于DRL的对手建模(DRL-OM)技术对复杂环境中其他智能体具有更好的认知能力,目前已在德州扑克[7-8]、星际争霸II[9]等多智能体问题场景取得优异的表现. ...
... 在即时策略类游戏中,2019年10月研究机构DeepMind提出了星际争霸II人工智能AlphaStar[8],面对异构智能体的策略学习问题,他们提出一种深度强化学习的联盟训练机制,从联盟中选取难以克服的对手作为陪练,发掘自身暴露的缺陷,以基于虚拟自博弈的显式DRL-OM方法学习历史最优策略. ...
An Opponent Modeling and Strategy Integration Framework for Texas Hold'em
2
2022
... 针对以上不足,研究者们将以深度Q网络(deep Q network, DQN)[6]为代表的深度强化学习算法(deep reinforcement learning, DRL)引入到对手建模领域.其中,强化学习是智能体学习如何与环境交互,达到最大化价值和最优策略的自主决策算法.深度学习则能够从高维感知数据中提取抽象特征,对复杂的价值函数和策略函数具有很强的拟合能力.DRL有机地结合了深度学习与强化学习,前者能够增强感知与表达能力,后者提供最优决策能力,使基于DRL的对手建模(DRL-OM)技术对复杂环境中其他智能体具有更好的认知能力,目前已在德州扑克[7-8]、星际争霸II[9]等多智能体问题场景取得优异的表现. ...
... 在即时策略类游戏中,2019年10月研究机构DeepMind提出了星际争霸II人工智能AlphaStar[8],面对异构智能体的策略学习问题,他们提出一种深度强化学习的联盟训练机制,从联盟中选取难以克服的对手作为陪练,发掘自身暴露的缺陷,以基于虚拟自博弈的显式DRL-OM方法学习历史最优策略. ...
Grandmaster Level in StarCraft II Using Multi-agent Reinforcement Learning
1
2019
... 针对以上不足,研究者们将以深度Q网络(deep Q network, DQN)[6]为代表的深度强化学习算法(deep reinforcement learning, DRL)引入到对手建模领域.其中,强化学习是智能体学习如何与环境交互,达到最大化价值和最优策略的自主决策算法.深度学习则能够从高维感知数据中提取抽象特征,对复杂的价值函数和策略函数具有很强的拟合能力.DRL有机地结合了深度学习与强化学习,前者能够增强感知与表达能力,后者提供最优决策能力,使基于DRL的对手建模(DRL-OM)技术对复杂环境中其他智能体具有更好的认知能力,目前已在德州扑克[7-8]、星际争霸II[9]等多智能体问题场景取得优异的表现. ...
Opponent Modelling for Case-Based Adaptive Game AI
2
2009
... DRL-OM是DRL方法在对手建模应用中的研究分支,涉及人工智能、神经科学、认知心理学、博弈论等众多领域.有别于以往的对手建模方法[10],DRL-OM研究涉及更复杂的应用场景、更多元的领域交叉,在问题特性、建模方式、应用场景上和传统方法具有较大差异.虽然许多现有文献[11-12]将对手建模领域的已有研究进行了汇总分类,但目前尚没有将基于DRL方法的对手建模进行系统研究的综述文章.此外,有关多智能体强化学习的综述研究[13-14]也阐述了对手建模的应用,然而它们的内容普遍较少涉及对手建模原理,也没有系统地分类和总结对手建模方法.随着DRL越来越广泛地应用在对手建模中,领域内涌现出许多崭新的理论和方法,远超现有文献总结的涵盖范围.因此,本文将DRL算法作为研究出发点,基于对手的理性程度和建模机理提出不同于现有文献[11-12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
... 现实应用中的即时决策场景十分常见,如竞技体育、战术决策等需要在短时间内做出反应决策.在强实时性的场景中,智能体面临着同时考虑计算准确性和效率的问题.Tang等[84]在滚动时域算法的基础上,使用深度强化学习预测对手行动,优化对手建模的有效性,实现了双人格斗游戏的博弈推理.然而,在多人在线游戏、大规模作战仿真等应用[10]中,面临的是多人实时博弈这种更为复杂的情况,实现这类场景下对手建模的实时性决策是亟需解决的难题. ...
面向多智能体博弈对抗的对手建模框架
2
2022
... DRL-OM是DRL方法在对手建模应用中的研究分支,涉及人工智能、神经科学、认知心理学、博弈论等众多领域.有别于以往的对手建模方法[10],DRL-OM研究涉及更复杂的应用场景、更多元的领域交叉,在问题特性、建模方式、应用场景上和传统方法具有较大差异.虽然许多现有文献[11-12]将对手建模领域的已有研究进行了汇总分类,但目前尚没有将基于DRL方法的对手建模进行系统研究的综述文章.此外,有关多智能体强化学习的综述研究[13-14]也阐述了对手建模的应用,然而它们的内容普遍较少涉及对手建模原理,也没有系统地分类和总结对手建模方法.随着DRL越来越广泛地应用在对手建模中,领域内涌现出许多崭新的理论和方法,远超现有文献总结的涵盖范围.因此,本文将DRL算法作为研究出发点,基于对手的理性程度和建模机理提出不同于现有文献[11-12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
... [11-12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
Research on Opponent Modeling Framework for Multi-agent Game Confrontation
2
2022
... DRL-OM是DRL方法在对手建模应用中的研究分支,涉及人工智能、神经科学、认知心理学、博弈论等众多领域.有别于以往的对手建模方法[10],DRL-OM研究涉及更复杂的应用场景、更多元的领域交叉,在问题特性、建模方式、应用场景上和传统方法具有较大差异.虽然许多现有文献[11-12]将对手建模领域的已有研究进行了汇总分类,但目前尚没有将基于DRL方法的对手建模进行系统研究的综述文章.此外,有关多智能体强化学习的综述研究[13-14]也阐述了对手建模的应用,然而它们的内容普遍较少涉及对手建模原理,也没有系统地分类和总结对手建模方法.随着DRL越来越广泛地应用在对手建模中,领域内涌现出许多崭新的理论和方法,远超现有文献总结的涵盖范围.因此,本文将DRL算法作为研究出发点,基于对手的理性程度和建模机理提出不同于现有文献[11-12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
... [11-12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
智能体对手建模研究进展
2
2021
... DRL-OM是DRL方法在对手建模应用中的研究分支,涉及人工智能、神经科学、认知心理学、博弈论等众多领域.有别于以往的对手建模方法[10],DRL-OM研究涉及更复杂的应用场景、更多元的领域交叉,在问题特性、建模方式、应用场景上和传统方法具有较大差异.虽然许多现有文献[11-12]将对手建模领域的已有研究进行了汇总分类,但目前尚没有将基于DRL方法的对手建模进行系统研究的综述文章.此外,有关多智能体强化学习的综述研究[13-14]也阐述了对手建模的应用,然而它们的内容普遍较少涉及对手建模原理,也没有系统地分类和总结对手建模方法.随着DRL越来越广泛地应用在对手建模中,领域内涌现出许多崭新的理论和方法,远超现有文献总结的涵盖范围.因此,本文将DRL算法作为研究出发点,基于对手的理性程度和建模机理提出不同于现有文献[11-12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
... -12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
Research Progress of Opponent Modeling for Agent
2
2021
... DRL-OM是DRL方法在对手建模应用中的研究分支,涉及人工智能、神经科学、认知心理学、博弈论等众多领域.有别于以往的对手建模方法[10],DRL-OM研究涉及更复杂的应用场景、更多元的领域交叉,在问题特性、建模方式、应用场景上和传统方法具有较大差异.虽然许多现有文献[11-12]将对手建模领域的已有研究进行了汇总分类,但目前尚没有将基于DRL方法的对手建模进行系统研究的综述文章.此外,有关多智能体强化学习的综述研究[13-14]也阐述了对手建模的应用,然而它们的内容普遍较少涉及对手建模原理,也没有系统地分类和总结对手建模方法.随着DRL越来越广泛地应用在对手建模中,领域内涌现出许多崭新的理论和方法,远超现有文献总结的涵盖范围.因此,本文将DRL算法作为研究出发点,基于对手的理性程度和建模机理提出不同于现有文献[11-12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
... -12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
A Survey and Critique of Multiagent Deep Reinforcement Learning
1
2019
... DRL-OM是DRL方法在对手建模应用中的研究分支,涉及人工智能、神经科学、认知心理学、博弈论等众多领域.有别于以往的对手建模方法[10],DRL-OM研究涉及更复杂的应用场景、更多元的领域交叉,在问题特性、建模方式、应用场景上和传统方法具有较大差异.虽然许多现有文献[11-12]将对手建模领域的已有研究进行了汇总分类,但目前尚没有将基于DRL方法的对手建模进行系统研究的综述文章.此外,有关多智能体强化学习的综述研究[13-14]也阐述了对手建模的应用,然而它们的内容普遍较少涉及对手建模原理,也没有系统地分类和总结对手建模方法.随着DRL越来越广泛地应用在对手建模中,领域内涌现出许多崭新的理论和方法,远超现有文献总结的涵盖范围.因此,本文将DRL算法作为研究出发点,基于对手的理性程度和建模机理提出不同于现有文献[11-12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
Multiagent Learning Paradigms
1
2017
... DRL-OM是DRL方法在对手建模应用中的研究分支,涉及人工智能、神经科学、认知心理学、博弈论等众多领域.有别于以往的对手建模方法[10],DRL-OM研究涉及更复杂的应用场景、更多元的领域交叉,在问题特性、建模方式、应用场景上和传统方法具有较大差异.虽然许多现有文献[11-12]将对手建模领域的已有研究进行了汇总分类,但目前尚没有将基于DRL方法的对手建模进行系统研究的综述文章.此外,有关多智能体强化学习的综述研究[13-14]也阐述了对手建模的应用,然而它们的内容普遍较少涉及对手建模原理,也没有系统地分类和总结对手建模方法.随着DRL越来越广泛地应用在对手建模中,领域内涌现出许多崭新的理论和方法,远超现有文献总结的涵盖范围.因此,本文将DRL算法作为研究出发点,基于对手的理性程度和建模机理提出不同于现有文献[11-12]的对手建模分类标准.此外,对手建模技术的更新迭代为现实应用提供了机遇和挑战,为此,本文汇总归纳了DRL-OM方法在应用领域的相关研究工作. ...
A Survey of Opponent Modeling in Adversarial Domains
1
2022
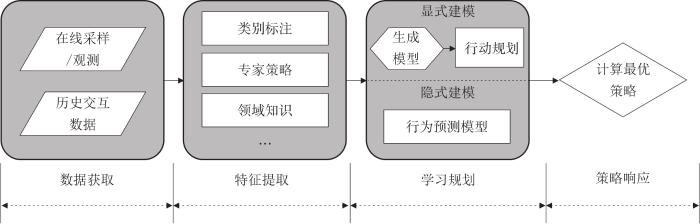
... 如图1所示,对手建模可以划分为数据获取、特征提取、学习规划、策略响应4个阶段[15].根据对手建模的应用目的,对手建模能在对抗场景中预测对手行为并予以回击,或利用对手策略上的疏漏获取更高收益.对手建模也可以在合作场景中建立团队成员的模型,在行动前予以配合,实现更为高效的任务协同. ...
Learning Against Opponents with Bounded Memory
1
2005
... 一般来说,对手建模方法可以分为显式对手建模和隐式对手建模.前者需要建立预测对手的行为模型或者推理过程.具体来说,显式建模从与对手的在线交互中获取数据,提取对手的行动、意图、信念特征,并且将对手特征预测和规划推理两部分解耦,便于直观分析.典型的显式对手建模方法有策略重构[16-17]、递归推理[18-19]、图模型[20-21]、群体建模[22-23]等.显式建模的优点是结果预测精准,模型可信性强.缺点是特征表示复杂,需要较强的先验知识用于设计模型架构. ...
Cooperating with A Markovian Ad Hoc Teammate
1
2013
... 一般来说,对手建模方法可以分为显式对手建模和隐式对手建模.前者需要建立预测对手的行为模型或者推理过程.具体来说,显式建模从与对手的在线交互中获取数据,提取对手的行动、意图、信念特征,并且将对手特征预测和规划推理两部分解耦,便于直观分析.典型的显式对手建模方法有策略重构[16-17]、递归推理[18-19]、图模型[20-21]、群体建模[22-23]等.显式建模的优点是结果预测精准,模型可信性强.缺点是特征表示复杂,需要较强的先验知识用于设计模型架构. ...
Negotiating with other Minds: The Role of Recursive Theory of Mind in Negotiation with Incomplete Information
1
2017
... 一般来说,对手建模方法可以分为显式对手建模和隐式对手建模.前者需要建立预测对手的行为模型或者推理过程.具体来说,显式建模从与对手的在线交互中获取数据,提取对手的行动、意图、信念特征,并且将对手特征预测和规划推理两部分解耦,便于直观分析.典型的显式对手建模方法有策略重构[16-17]、递归推理[18-19]、图模型[20-21]、群体建模[22-23]等.显式建模的优点是结果预测精准,模型可信性强.缺点是特征表示复杂,需要较强的先验知识用于设计模型架构. ...
Scalable Solutions of Interactive POMDPs Using Generalized and Bounded Policy Iteration
1
2015
... 一般来说,对手建模方法可以分为显式对手建模和隐式对手建模.前者需要建立预测对手的行为模型或者推理过程.具体来说,显式建模从与对手的在线交互中获取数据,提取对手的行动、意图、信念特征,并且将对手特征预测和规划推理两部分解耦,便于直观分析.典型的显式对手建模方法有策略重构[16-17]、递归推理[18-19]、图模型[20-21]、群体建模[22-23]等.显式建模的优点是结果预测精准,模型可信性强.缺点是特征表示复杂,需要较强的先验知识用于设计模型架构. ...
Exploiting Model Equivalences for Solving Interactive Dynamic Influence Diagrams
1
2012
... 一般来说,对手建模方法可以分为显式对手建模和隐式对手建模.前者需要建立预测对手的行为模型或者推理过程.具体来说,显式建模从与对手的在线交互中获取数据,提取对手的行动、意图、信念特征,并且将对手特征预测和规划推理两部分解耦,便于直观分析.典型的显式对手建模方法有策略重构[16-17]、递归推理[18-19]、图模型[20-21]、群体建模[22-23]等.显式建模的优点是结果预测精准,模型可信性强.缺点是特征表示复杂,需要较强的先验知识用于设计模型架构. ...
Graphical Models for Interactive POMDPs: Representations and Solutions
1
2009
... 一般来说,对手建模方法可以分为显式对手建模和隐式对手建模.前者需要建立预测对手的行为模型或者推理过程.具体来说,显式建模从与对手的在线交互中获取数据,提取对手的行动、意图、信念特征,并且将对手特征预测和规划推理两部分解耦,便于直观分析.典型的显式对手建模方法有策略重构[16-17]、递归推理[18-19]、图模型[20-21]、群体建模[22-23]等.显式建模的优点是结果预测精准,模型可信性强.缺点是特征表示复杂,需要较强的先验知识用于设计模型架构. ...
Cooperating with Unknown Teammates in Complex Domains: A Robot Soccer Case Study of ad Hoc Teamwork
1
2015
... 一般来说,对手建模方法可以分为显式对手建模和隐式对手建模.前者需要建立预测对手的行为模型或者推理过程.具体来说,显式建模从与对手的在线交互中获取数据,提取对手的行动、意图、信念特征,并且将对手特征预测和规划推理两部分解耦,便于直观分析.典型的显式对手建模方法有策略重构[16-17]、递归推理[18-19]、图模型[20-21]、群体建模[22-23]等.显式建模的优点是结果预测精准,模型可信性强.缺点是特征表示复杂,需要较强的先验知识用于设计模型架构. ...
Action Selection via Learning Behavior Patterns in Multi-Robot Systems
1
2011
... 一般来说,对手建模方法可以分为显式对手建模和隐式对手建模.前者需要建立预测对手的行为模型或者推理过程.具体来说,显式建模从与对手的在线交互中获取数据,提取对手的行动、意图、信念特征,并且将对手特征预测和规划推理两部分解耦,便于直观分析.典型的显式对手建模方法有策略重构[16-17]、递归推理[18-19]、图模型[20-21]、群体建模[22-23]等.显式建模的优点是结果预测精准,模型可信性强.缺点是特征表示复杂,需要较强的先验知识用于设计模型架构. ...
A Data Mining Approach to Strategy Prediction
1
2009
... 与显式建模方法相对,隐式建模不是建立其他智能体的显式模型,而是在自身结构或推理过程中含蓄地编码对手智能体,例如,将建模和规划合为一体或者将捕获的对手行为特征蕴含在机器学习模型的优化目标中.隐式建模方法可以通过对手交互的历史数据离线训练,避免了在线计算资源开销大、决策时延长的问题.典型的方法包括特征聚类[24-25]、神经网络预测[26]、意图识别[27-29]、类别推理[30-31]等.隐式对手建模避免了在线计算和先验知识要求,有利于在信息不完全的情况下决策.缺点是由于无法有效衡量学到的行为预测模型和真实之间的差异,导致难以权衡模型的探索和利用问题. ...
Opponent Modeling in Real-Time Strategy Games
1
2007
... 与显式建模方法相对,隐式建模不是建立其他智能体的显式模型,而是在自身结构或推理过程中含蓄地编码对手智能体,例如,将建模和规划合为一体或者将捕获的对手行为特征蕴含在机器学习模型的优化目标中.隐式建模方法可以通过对手交互的历史数据离线训练,避免了在线计算资源开销大、决策时延长的问题.典型的方法包括特征聚类[24-25]、神经网络预测[26]、意图识别[27-29]、类别推理[30-31]等.隐式对手建模避免了在线计算和先验知识要求,有利于在信息不完全的情况下决策.缺点是由于无法有效衡量学到的行为预测模型和真实之间的差异,导致难以权衡模型的探索和利用问题. ...
Opponent Modeling in Deep Reinforcement Learning
5
2016
... 与显式建模方法相对,隐式建模不是建立其他智能体的显式模型,而是在自身结构或推理过程中含蓄地编码对手智能体,例如,将建模和规划合为一体或者将捕获的对手行为特征蕴含在机器学习模型的优化目标中.隐式建模方法可以通过对手交互的历史数据离线训练,避免了在线计算资源开销大、决策时延长的问题.典型的方法包括特征聚类[24-25]、神经网络预测[26]、意图识别[27-29]、类别推理[30-31]等.隐式对手建模避免了在线计算和先验知识要求,有利于在信息不完全的情况下决策.缺点是由于无法有效衡量学到的行为预测模型和真实之间的差异,导致难以权衡模型的探索和利用问题. ...
... 辅助任务是一种多任务的DRL方法[70],为智能体提供了更丰富的行为动机,适合非平稳环境的学习任务.辅助任务的建模方法设计获取对手特征的模型,修正强化学习的策略和价值函数,为强化学习提供与对手博弈的行为动机.该方法将其他智能体的观测编码作为监督信息输入神经网络进行训练,提取对手策略特征,用于修正强化学习的策略和价值函数,完成最大化奖励的目标[26,71-72].这类方法中具有开创性的工作是He等[26]提出的深度强化对手网络(deep reinforcement opponent network, DRON).在多智能体系统中,对手的行动将会改变环境状态转移,从而影响智能体强化学习过程的收敛性.因此,DRON同时训练Q值网络和对手策略表征网络,将对手策略表征作为环境已知条件帮助Q值网络收敛.在具体实现中,DRON在DQN的基础上改造,使用一个网络评估Q值,另一个网络则负责对手建模,以对手的行动作为输入,捕获当前对手的特征,用于学习对手策略.在此基础上,它结合多个专家网络预测估计Q值,每个专家网络捕获一种对手策略.在1v1足球比赛场景下DRON智能体与基于规则的对手智能体对抗训练,DRON智能体赢得了99.86%的进攻,并且防守成功不低于90.20%.该方法的缺点是专家网络的模型和输入需要依据先验知识手工设定. ...
... [26]提出的深度强化对手网络(deep reinforcement opponent network, DRON).在多智能体系统中,对手的行动将会改变环境状态转移,从而影响智能体强化学习过程的收敛性.因此,DRON同时训练Q值网络和对手策略表征网络,将对手策略表征作为环境已知条件帮助Q值网络收敛.在具体实现中,DRON在DQN的基础上改造,使用一个网络评估Q值,另一个网络则负责对手建模,以对手的行动作为输入,捕获当前对手的特征,用于学习对手策略.在此基础上,它结合多个专家网络预测估计Q值,每个专家网络捕获一种对手策略.在1v1足球比赛场景下DRON智能体与基于规则的对手智能体对抗训练,DRON智能体赢得了99.86%的进攻,并且防守成功不低于90.20%.该方法的缺点是专家网络的模型和输入需要依据先验知识手工设定. ...
... Summary of research motivation, innovation points and limitations of implicit based opponent modeling methods
Table 4| 类别 | 算法 | 研究动机 | 模型特点 | 创新点 | 局限性 |
|---|
| 辅助 任务 | DRON[26] | 设计挖掘不同对手策略隐藏特征的神经网络 | 使用MLP处理对手行动,将表征信息用于强化学习任务 | 提取对手特征用于DRL算法决策 | 手工提取输入专家网络的特征,可采用RNN改进 |
| DIPQN[71] | 从观测直接提取对手策略特征,训练对手建模的辅助任务 | 策略特征网络学习从观测提取表征,并通过行为克隆的准确性修正网络 | 设计了调节最大奖励与对手建模的自适应损失函数 | 采用经验回放池离线训练,学习的对手策略具有较大样本方差 |
| AMS-A3C[72] | 在强化学习过程中,制订估计其他智能体策略的辅助任务 | 决策网络与模仿决策的对手模型共享结构、参数,降低模型学习成本 | 提出参数共享、策略表征2套方案,将对手建模融合进A3C算法 | 对手模型参数敏感,难以应对复杂场景、具有学习能力的对手 |
| 学习 表征 | PPO-Emb[74] | 从交互样本中无监督地学习对手表征 | 提取同时具有策略提升效果和对手区分度的表征信息 | 无需领域知识,通用性强,适用大多数DRL算法 | 无法独立推断,用于辅助其他DRL算法决策 |
| RFM[73] | 采用图网络学习智能体的社会关系表征 | 通过边缘属性、节点等图结构信息预测对手行动、评估对手社会关系强度 | 量化智能体交互的社会属性,网络结构具有较好拓展性 | 存在复杂交互关系的图网络计算困难 |
| 概率 推理 | P-BIT[76] | 多智能体DRL的最优策略形式化为推理私有信息的概率下界 | 使用信念模块根据友方行为推理其私有信息 | 提出不完美信息条件下通过行动与队友传递私有信息的方法 | 适用于简单的二人合作场景 |
| ROMMEO[78] | 多智能体DRL形式化为基于对手模型的最优策略变分推理 | 预测对手行动,用于实现学习最优策略的推理任务 | 提出最大熵目标的正则化的对手建模方法 | 在线优化参数,训练时间长.默认对手目标已知,无法适应未知智能体 |
| 自我- 他人交互 | SOM[79] | 基于自身策略推理对手可能的目标,用于支撑决策 | 建立拟合对手策略的神经网络,通过优化对手策略反向推断对手的目标 | 无需额外模型和参数显式建模,仿照自身模型推理任意数量规模对手 | 智能体与对手共享目标,并且奖励结构取决于目标 |
| LOLA[81] | 考虑具有学习能力的对手,解释对手学习参数的更新对自身策略影响 | 建模对手的价值函数,求其二阶导优化策略梯度 | 策略更新中增加了对手参数更新项,通过泰勒展开构造成高阶梯度项 | 默认对手使用可梯度优化的方法,并且无法察觉LOLA对其模型进行利用 |
4 应用场景DRL-OM方法起初应用于游戏领域的智能体建模,随着深度强化学习算法在现实场景中的落地应用,DRL-OM技术也拓展到军事仿真、公共安全等诸多领域. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Bayesian Theory of Mind: Modeling Joint Belief-desire Attribution
1
2011
... 与显式建模方法相对,隐式建模不是建立其他智能体的显式模型,而是在自身结构或推理过程中含蓄地编码对手智能体,例如,将建模和规划合为一体或者将捕获的对手行为特征蕴含在机器学习模型的优化目标中.隐式建模方法可以通过对手交互的历史数据离线训练,避免了在线计算资源开销大、决策时延长的问题.典型的方法包括特征聚类[24-25]、神经网络预测[26]、意图识别[27-29]、类别推理[30-31]等.隐式对手建模避免了在线计算和先验知识要求,有利于在信息不完全的情况下决策.缺点是由于无法有效衡量学到的行为预测模型和真实之间的差异,导致难以权衡模型的探索和利用问题. ...
A Computational Decision Theory for Interactive Assistants
0
2010
Plan Recognition as Planning Revisited
1
2016
... 与显式建模方法相对,隐式建模不是建立其他智能体的显式模型,而是在自身结构或推理过程中含蓄地编码对手智能体,例如,将建模和规划合为一体或者将捕获的对手行为特征蕴含在机器学习模型的优化目标中.隐式建模方法可以通过对手交互的历史数据离线训练,避免了在线计算资源开销大、决策时延长的问题.典型的方法包括特征聚类[24-25]、神经网络预测[26]、意图识别[27-29]、类别推理[30-31]等.隐式对手建模避免了在线计算和先验知识要求,有利于在信息不完全的情况下决策.缺点是由于无法有效衡量学到的行为预测模型和真实之间的差异,导致难以权衡模型的探索和利用问题. ...
Reasoning about Hypothetical Agent Behaviours and Their Parameters
1
2017
... 与显式建模方法相对,隐式建模不是建立其他智能体的显式模型,而是在自身结构或推理过程中含蓄地编码对手智能体,例如,将建模和规划合为一体或者将捕获的对手行为特征蕴含在机器学习模型的优化目标中.隐式建模方法可以通过对手交互的历史数据离线训练,避免了在线计算资源开销大、决策时延长的问题.典型的方法包括特征聚类[24-25]、神经网络预测[26]、意图识别[27-29]、类别推理[30-31]等.隐式对手建模避免了在线计算和先验知识要求,有利于在信息不完全的情况下决策.缺点是由于无法有效衡量学到的行为预测模型和真实之间的差异,导致难以权衡模型的探索和利用问题. ...
Belief and Truth in Hypothesised Behaviours
1
2016
... 与显式建模方法相对,隐式建模不是建立其他智能体的显式模型,而是在自身结构或推理过程中含蓄地编码对手智能体,例如,将建模和规划合为一体或者将捕获的对手行为特征蕴含在机器学习模型的优化目标中.隐式建模方法可以通过对手交互的历史数据离线训练,避免了在线计算资源开销大、决策时延长的问题.典型的方法包括特征聚类[24-25]、神经网络预测[26]、意图识别[27-29]、类别推理[30-31]等.隐式对手建模避免了在线计算和先验知识要求,有利于在信息不完全的情况下决策.缺点是由于无法有效衡量学到的行为预测模型和真实之间的差异,导致难以权衡模型的探索和利用问题. ...
多智能体深度强化学习的若干关键科学问题
1
2020
... 在强化学习方法的基础上,DRL将深度神经网络(deep neural network, DNN)作为价值和策略的近似函数,提升了高维输入数据下的特征提取能力.DRL方法主要分为两大类[32]:值函数近似方法和策略梯度方法.值函数近似方法通过神经网络梯度下降逼近动作价值函数,缺点是容易收敛到局部最优点,难以处理连续动作空间的任务;策略梯度方法是将策略参数化,通过深度神经网络逼近策略函数,再沿着策略梯度方向求解最优策略. ...
Important Scientific Problems of Multi-Agent Deep Reinforcement Learning
1
2020
... 在强化学习方法的基础上,DRL将深度神经网络(deep neural network, DNN)作为价值和策略的近似函数,提升了高维输入数据下的特征提取能力.DRL方法主要分为两大类[32]:值函数近似方法和策略梯度方法.值函数近似方法通过神经网络梯度下降逼近动作价值函数,缺点是容易收敛到局部最优点,难以处理连续动作空间的任务;策略梯度方法是将策略参数化,通过深度神经网络逼近策略函数,再沿着策略梯度方向求解最优策略. ...
Deep Recurrent Q-Learning for Partially Observable MDPs
2
2015
... DQN存在诸多不足,如经验回放池容量有限、需要完整观测信息.深度循环Q网络(deep recurrent Q network, DRQN)[33]使用长短时记忆网络代替全连接层网络,用于解决部分可观测条件下的决策问题. ...
... Deep reinforcement learning algorithms in OM
Table 1| 分类 | 算法 | 优点 | 不足 |
|---|
| 值函数近似 | DQN[6] | 经验复用、离轨策略机制 | 无法用于高维、连续空间 |
| DRQN[33] | 采用LSTM代替全连接层 | 完全可观测下表现不如DQN |
| 策略梯度 | DDPG[34] | 确定性策略、Actor-Critic框架 | 无法处理离散问题、难以确定更新步长 |
| A3C[35] | 多线程学习、异步更新参数 | 更新策略方差较大 |
| PPO[37] | 有裁剪的自适应超参数KL散度 | 对差异性较大样本敏感 |
2 基于DRL的显式对手建模按照对手的理性程度和建模机理,基于DRL的显式对手建模的主要方法可以分为博弈均衡策略建模方法和递归推理建模方法.博弈均衡策略方法主张对手的绝对理性,采用博弈论的均衡原理建模,递归推理方法强调了智能体具备有限理性,从认知心理学的人类理性研究中获取灵感. ...
Continuous Control with Deep Reinforcement Learning
2
1509
... DQN无法处理连续动作控制任务,因此Lillicrap等[34]在确定性梯度理论基础上结合Actor-Critic框架提出了深度确定性策略梯度算法(deep deterministic policy gradient algorithms, DDPG).DDPG将动作策略和动作策略探索的学习更新分离,执行动作策略时使用确定性策略,探索时使用随机策略.类似于DQN,DDPG训练时从经验回放池中采样,对目标网络和预测网络进行离线策略更新.每个网络采用Actor-Critic结构,分别进行策略更新和值函数更新,使Q网络更容易收敛. ...
... Deep reinforcement learning algorithms in OM
Table 1| 分类 | 算法 | 优点 | 不足 |
|---|
| 值函数近似 | DQN[6] | 经验复用、离轨策略机制 | 无法用于高维、连续空间 |
| DRQN[33] | 采用LSTM代替全连接层 | 完全可观测下表现不如DQN |
| 策略梯度 | DDPG[34] | 确定性策略、Actor-Critic框架 | 无法处理离散问题、难以确定更新步长 |
| A3C[35] | 多线程学习、异步更新参数 | 更新策略方差较大 |
| PPO[37] | 有裁剪的自适应超参数KL散度 | 对差异性较大样本敏感 |
2 基于DRL的显式对手建模按照对手的理性程度和建模机理,基于DRL的显式对手建模的主要方法可以分为博弈均衡策略建模方法和递归推理建模方法.博弈均衡策略方法主张对手的绝对理性,采用博弈论的均衡原理建模,递归推理方法强调了智能体具备有限理性,从认知心理学的人类理性研究中获取灵感. ...
Asynchronous Methods for Deep Reinforcement Learning
2
2016
... 根据异步强化学习的思想,Mnih等[35]提出异步优势演员-评论家算法(asynchronous advantage actor-critic, A3C).A3C创建多线程同步训练,演员-评论家框架的智能体在相互间不干扰的并行环境中更新参数.A3C是多个worker从环境副本中收集经验,计算梯度之后,将梯度上传给主网络,更新主网络,并下载最新的主网络副本.避免了单一智能体连续提交更新的问题,以此降低样本相关性,提高收敛能力. ...
... Deep reinforcement learning algorithms in OM
Table 1| 分类 | 算法 | 优点 | 不足 |
|---|
| 值函数近似 | DQN[6] | 经验复用、离轨策略机制 | 无法用于高维、连续空间 |
| DRQN[33] | 采用LSTM代替全连接层 | 完全可观测下表现不如DQN |
| 策略梯度 | DDPG[34] | 确定性策略、Actor-Critic框架 | 无法处理离散问题、难以确定更新步长 |
| A3C[35] | 多线程学习、异步更新参数 | 更新策略方差较大 |
| PPO[37] | 有裁剪的自适应超参数KL散度 | 对差异性较大样本敏感 |
2 基于DRL的显式对手建模按照对手的理性程度和建模机理,基于DRL的显式对手建模的主要方法可以分为博弈均衡策略建模方法和递归推理建模方法.博弈均衡策略方法主张对手的绝对理性,采用博弈论的均衡原理建模,递归推理方法强调了智能体具备有限理性,从认知心理学的人类理性研究中获取灵感. ...
Trust Region Policy Optimization
1
2015
... 策略梯度方法具有选择更新步长的问题.步长过短会增加迭代耗时,而过长会导致更新到差策略,差策略产生的数据导致策略进一步变差,最终模型效果不佳.Schulman等[36]提出信任域策略优化算法,在策略更新中选择合适的步长,保证奖励函数单调增加.近端策略优化(proximal policy optimization, PPO)[37]在信任域策略优化算法的基础上使用一阶优化代替强约束,降低策略更新前后的分布差异性,解决了一般信任域优化算法运算复杂问题. ...
Proximal Policy Optimization Algorithms
2
1707
... 策略梯度方法具有选择更新步长的问题.步长过短会增加迭代耗时,而过长会导致更新到差策略,差策略产生的数据导致策略进一步变差,最终模型效果不佳.Schulman等[36]提出信任域策略优化算法,在策略更新中选择合适的步长,保证奖励函数单调增加.近端策略优化(proximal policy optimization, PPO)[37]在信任域策略优化算法的基础上使用一阶优化代替强约束,降低策略更新前后的分布差异性,解决了一般信任域优化算法运算复杂问题. ...
... Deep reinforcement learning algorithms in OM
Table 1| 分类 | 算法 | 优点 | 不足 |
|---|
| 值函数近似 | DQN[6] | 经验复用、离轨策略机制 | 无法用于高维、连续空间 |
| DRQN[33] | 采用LSTM代替全连接层 | 完全可观测下表现不如DQN |
| 策略梯度 | DDPG[34] | 确定性策略、Actor-Critic框架 | 无法处理离散问题、难以确定更新步长 |
| A3C[35] | 多线程学习、异步更新参数 | 更新策略方差较大 |
| PPO[37] | 有裁剪的自适应超参数KL散度 | 对差异性较大样本敏感 |
2 基于DRL的显式对手建模按照对手的理性程度和建模机理,基于DRL的显式对手建模的主要方法可以分为博弈均衡策略建模方法和递归推理建模方法.博弈均衡策略方法主张对手的绝对理性,采用博弈论的均衡原理建模,递归推理方法强调了智能体具备有限理性,从认知心理学的人类理性研究中获取灵感. ...
Fictitious Self-play in Extensive-form Games
3
2015
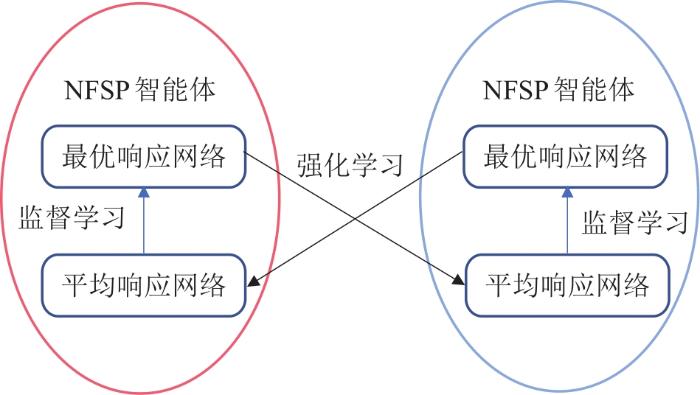
... 虚拟自博弈[38]的主要思想是在扩展式博弈中跟踪对手的历史行为,并根据对手的平均策略选择最佳对策.神经虚拟自博弈(neural fictitious self-play, NFSP)[39-41]以虚拟自博弈为基础,利用深度神经网络拓展了不完全信息博弈的研究,并在诸如扑克的场景下达到近似纳什均衡.如图2所示,NFSP的最佳反应依赖于最佳响应网络和历史平均网络.最佳响应网络的实现是基于DQN,以ϵ-贪婪的策略探索行为奖励,学习Q值得到对其他智能体历史行为的最佳响应.历史平均网络是模仿对手智能体历史最佳响应的对手模型,使用多层神经网络通过监督学习实现对从状态到行为的对手策略映射.在不完全信息博弈的二人德州扑克游戏中,NFSP智能体能够在没有领域先验知识的情况下收敛至近似纳什均衡.然而基于DQN的最优响应在对手策略变化的博弈中难以收敛,并且面临在搜索规模巨大、搜索深度较深的场景学习困难等问题.针对NFSP无法收敛最优的问题,Zhang等[41]提出将蒙特卡罗树与NFSP相结合,以在线更新策略的蒙特卡罗搜索的方式训练,解决了DQN无法近似最优解的问题,缺点是蒙特卡罗搜索存在产生样本方差大的问题. ...
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Deep Reinforcement Learning from Self-play in Imperfect-Information Games
2
1603
... 虚拟自博弈[38]的主要思想是在扩展式博弈中跟踪对手的历史行为,并根据对手的平均策略选择最佳对策.神经虚拟自博弈(neural fictitious self-play, NFSP)[39-41]以虚拟自博弈为基础,利用深度神经网络拓展了不完全信息博弈的研究,并在诸如扑克的场景下达到近似纳什均衡.如图2所示,NFSP的最佳反应依赖于最佳响应网络和历史平均网络.最佳响应网络的实现是基于DQN,以ϵ-贪婪的策略探索行为奖励,学习Q值得到对其他智能体历史行为的最佳响应.历史平均网络是模仿对手智能体历史最佳响应的对手模型,使用多层神经网络通过监督学习实现对从状态到行为的对手策略映射.在不完全信息博弈的二人德州扑克游戏中,NFSP智能体能够在没有领域先验知识的情况下收敛至近似纳什均衡.然而基于DQN的最优响应在对手策略变化的博弈中难以收敛,并且面临在搜索规模巨大、搜索深度较深的场景学习困难等问题.针对NFSP无法收敛最优的问题,Zhang等[41]提出将蒙特卡罗树与NFSP相结合,以在线更新策略的蒙特卡罗搜索的方式训练,解决了DQN无法近似最优解的问题,缺点是蒙特卡罗搜索存在产生样本方差大的问题. ...
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
Neural Fictitious Self-play on ELF Mini-rts
1
1902
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
A Monte Carlo Neural Fictitious Self-Play Approach to Approximate Nash Equilibrium in Imperfect-information Dynamic Games
2
2021
... 虚拟自博弈[38]的主要思想是在扩展式博弈中跟踪对手的历史行为,并根据对手的平均策略选择最佳对策.神经虚拟自博弈(neural fictitious self-play, NFSP)[39-41]以虚拟自博弈为基础,利用深度神经网络拓展了不完全信息博弈的研究,并在诸如扑克的场景下达到近似纳什均衡.如图2所示,NFSP的最佳反应依赖于最佳响应网络和历史平均网络.最佳响应网络的实现是基于DQN,以ϵ-贪婪的策略探索行为奖励,学习Q值得到对其他智能体历史行为的最佳响应.历史平均网络是模仿对手智能体历史最佳响应的对手模型,使用多层神经网络通过监督学习实现对从状态到行为的对手策略映射.在不完全信息博弈的二人德州扑克游戏中,NFSP智能体能够在没有领域先验知识的情况下收敛至近似纳什均衡.然而基于DQN的最优响应在对手策略变化的博弈中难以收敛,并且面临在搜索规模巨大、搜索深度较深的场景学习困难等问题.针对NFSP无法收敛最优的问题,Zhang等[41]提出将蒙特卡罗树与NFSP相结合,以在线更新策略的蒙特卡罗搜索的方式训练,解决了DQN无法近似最优解的问题,缺点是蒙特卡罗搜索存在产生样本方差大的问题. ...
... [41]提出将蒙特卡罗树与NFSP相结合,以在线更新策略的蒙特卡罗搜索的方式训练,解决了DQN无法近似最优解的问题,缺点是蒙特卡罗搜索存在产生样本方差大的问题. ...
A Unified Game-Theoretic Approach to Multiagent Reinforcement Learning
3
2017
... (policy-space response oracles, PSRO)[42]是在NFSP的概念上进一步推广,证明虚拟博弈是以先前近似最佳反应为依据的一个特定元策略分布.假定元策略并非唯一,PSRO通过基于线性规划、虚拟博弈、遗憾值最小化等算法实现的元策略求解器为每个智能体依次选择混合元策略.当每个智能体计算当前的元策略时,同时基于对手智能体的元策略集进行概率抽样,获得对手的混合策略,并据此计算最优响应策略更新元策略集.这类方法防止对特定策略的响应过度拟合,从而提供了一种对手规范化的形式.由于PSRO算法与行为博弈论模型的相似性,该算法又产生了一个独立的近似扩展版本,计算智能体的最佳响应,称为深度认知层次.在多玩家博弈中,PSRO计算纳什均衡常面临均衡选择问题.-rank[43]是一种用于大规模多智能体交互中评估和排序智能体的进化动力学方法.Muller等[44-45]将-rank方法应用在PSRO算法中,结合卡尔科夫-康尼链作为评价解概念.马尔科夫-康尼链刻画智能体种群的长期动态,作为评估对手优劣势的标准,使一般和多玩家博弈中包括非纳什均衡策略的所有策略得到充分训练改进. ...
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
α-rank: Multi-agent Evaluation by Evolution
3
2019
... (policy-space response oracles, PSRO)[42]是在NFSP的概念上进一步推广,证明虚拟博弈是以先前近似最佳反应为依据的一个特定元策略分布.假定元策略并非唯一,PSRO通过基于线性规划、虚拟博弈、遗憾值最小化等算法实现的元策略求解器为每个智能体依次选择混合元策略.当每个智能体计算当前的元策略时,同时基于对手智能体的元策略集进行概率抽样,获得对手的混合策略,并据此计算最优响应策略更新元策略集.这类方法防止对特定策略的响应过度拟合,从而提供了一种对手规范化的形式.由于PSRO算法与行为博弈论模型的相似性,该算法又产生了一个独立的近似扩展版本,计算智能体的最佳响应,称为深度认知层次.在多玩家博弈中,PSRO计算纳什均衡常面临均衡选择问题.-rank[43]是一种用于大规模多智能体交互中评估和排序智能体的进化动力学方法.Muller等[44-45]将-rank方法应用在PSRO算法中,结合卡尔科夫-康尼链作为评价解概念.马尔科夫-康尼链刻画智能体种群的长期动态,作为评估对手优劣势的标准,使一般和多玩家博弈中包括非纳什均衡策略的所有策略得到充分训练改进. ...
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
... 非平稳性是指对手策略、环境状态转移、环境奖励不断发生变化,从而打破了MDP环境的马尔科夫性质,使得智能体无法学习到稳定的最优策略[117].诸如部分可观测、环境动态变化、对手策略学习等因素都会导致智能体的学习环境非平稳.因此,非平稳性智能体需要权衡模型学习潜在误差所导致的不确定性和在不确定性下的对手模型利用.例如,智能体无法获取对手当前的状态和动作信息,只能利用自身局部信息进行推理.为此,研究者通过无监督学习[118-119]从自身观测中提取被建模者的历史轨迹特征,建立对手模型.Papoudakis等[112-113]基于局部信息建模,采用变分自编码器(variational autoencoders, VAEs)学习历史轨迹的策略表征,并将其用于A3C算法的决策过程.然而,在智能体共同学习、智能种群演化等复杂动态问题中[43],策略难以收敛到静态最优,智能体陷入不断学习的循环.解决这类复杂任务中的非平稳性也是DRL-OM方法尚未解决的难题. ...
A Generalized Training Approach for Multiagent Learning
2
1909
... (policy-space response oracles, PSRO)[42]是在NFSP的概念上进一步推广,证明虚拟博弈是以先前近似最佳反应为依据的一个特定元策略分布.假定元策略并非唯一,PSRO通过基于线性规划、虚拟博弈、遗憾值最小化等算法实现的元策略求解器为每个智能体依次选择混合元策略.当每个智能体计算当前的元策略时,同时基于对手智能体的元策略集进行概率抽样,获得对手的混合策略,并据此计算最优响应策略更新元策略集.这类方法防止对特定策略的响应过度拟合,从而提供了一种对手规范化的形式.由于PSRO算法与行为博弈论模型的相似性,该算法又产生了一个独立的近似扩展版本,计算智能体的最佳响应,称为深度认知层次.在多玩家博弈中,PSRO计算纳什均衡常面临均衡选择问题.-rank[43]是一种用于大规模多智能体交互中评估和排序智能体的进化动力学方法.Muller等[44-45]将-rank方法应用在PSRO算法中,结合卡尔科夫-康尼链作为评价解概念.马尔科夫-康尼链刻画智能体种群的长期动态,作为评估对手优劣势的标准,使一般和多玩家博弈中包括非纳什均衡策略的所有策略得到充分训练改进. ...
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
Open-ended Learning in Symmetric Zero-sum Games
1
2019
... (policy-space response oracles, PSRO)[42]是在NFSP的概念上进一步推广,证明虚拟博弈是以先前近似最佳反应为依据的一个特定元策略分布.假定元策略并非唯一,PSRO通过基于线性规划、虚拟博弈、遗憾值最小化等算法实现的元策略求解器为每个智能体依次选择混合元策略.当每个智能体计算当前的元策略时,同时基于对手智能体的元策略集进行概率抽样,获得对手的混合策略,并据此计算最优响应策略更新元策略集.这类方法防止对特定策略的响应过度拟合,从而提供了一种对手规范化的形式.由于PSRO算法与行为博弈论模型的相似性,该算法又产生了一个独立的近似扩展版本,计算智能体的最佳响应,称为深度认知层次.在多玩家博弈中,PSRO计算纳什均衡常面临均衡选择问题.-rank[43]是一种用于大规模多智能体交互中评估和排序智能体的进化动力学方法.Muller等[44-45]将-rank方法应用在PSRO算法中,结合卡尔科夫-康尼链作为评价解概念.马尔科夫-康尼链刻画智能体种群的长期动态,作为评估对手优劣势的标准,使一般和多玩家博弈中包括非纳什均衡策略的所有策略得到充分训练改进. ...
Regret Minimization in Games with Incomplete Information
1
2007
... 虚拟自博弈的方法需要在真实对手交互中学习策略,然而许多应用场景无法满足与对手多次交互训练的前提条件.研究人员利用模拟的方法解决该问题,Martin等[46]提出的反事实遗憾值最小化是利用自我博弈来最小化反事实遗憾从而拟合纳什均衡的方法,能够很好地模拟扩展式博弈的树分支节点,并在扑克游戏中取得成功.它的流程是对所有信息集进行遗憾匹配计算,更新平均策略集并计算玩家的反事实收益值,最后使用反事实收益更新累计遗憾值.然而记录所有节点的累计遗憾值导致算法的计算和存储开销巨大.遗憾匹配计算式为 ...
Regret Minimization in Games and the Development of Champion Multiplayer Computer Poker-Playing Agents
1
2014
... 为解决最小化反事实遗憾值方法计算速度问题,研究者们从其原理出发提出一系列在线学习方法[47-51].Lanctot等[48]采用蒙特卡罗采样方式对博弈树进行部分抽样,相较原方法计算效率提升10倍,并且证明抽样更新的遗憾收益值是真实值的无偏估计.Tammelin[51]将平均策略的收益加以衰减,提高了近期迭代策略的权重.针对CFR算法的存储效率问题,研究者们也提出状态空间压缩和问题抽象方法[52-53].研究者也尝试对CFR方法的时效性问题和简化问题规模提出解法.王鹏程[54]提出适用于强化学习的模式匹配扑克建模方法,基于蒙特卡罗博弈树搜索计算回报函数,利用基于长短时记忆网络的DQN学习特征,降低了博弈问题求解难度.在非完全信息条件下,基于CFR方法的智能体在决策时建模对手可能采取的所有行动,将其表示为一个信息集,并学习使信息集遗憾值最小的自身策略. ...
Efficient Nash Equilibrium Approximation through Monte Carlo Counterfactual Regret Minimization
2
2012
... 为解决最小化反事实遗憾值方法计算速度问题,研究者们从其原理出发提出一系列在线学习方法[47-51].Lanctot等[48]采用蒙特卡罗采样方式对博弈树进行部分抽样,相较原方法计算效率提升10倍,并且证明抽样更新的遗憾收益值是真实值的无偏估计.Tammelin[51]将平均策略的收益加以衰减,提高了近期迭代策略的权重.针对CFR算法的存储效率问题,研究者们也提出状态空间压缩和问题抽象方法[52-53].研究者也尝试对CFR方法的时效性问题和简化问题规模提出解法.王鹏程[54]提出适用于强化学习的模式匹配扑克建模方法,基于蒙特卡罗博弈树搜索计算回报函数,利用基于长短时记忆网络的DQN学习特征,降低了博弈问题求解难度.在非完全信息条件下,基于CFR方法的智能体在决策时建模对手可能采取的所有行动,将其表示为一个信息集,并学习使信息集遗憾值最小的自身策略. ...
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
Monte Carlo Sampling and Regret Minimization for Equilibrium Computation and Decision-Making in Large Extensive Form Games
0
2013
Reduced Space and Faster Convergence in Imperfect-information Games via Pruning
0
2017
Solving Large Imperfect Information Games Using CFR+
3
1407
... 为解决最小化反事实遗憾值方法计算速度问题,研究者们从其原理出发提出一系列在线学习方法[47-51].Lanctot等[48]采用蒙特卡罗采样方式对博弈树进行部分抽样,相较原方法计算效率提升10倍,并且证明抽样更新的遗憾收益值是真实值的无偏估计.Tammelin[51]将平均策略的收益加以衰减,提高了近期迭代策略的权重.针对CFR算法的存储效率问题,研究者们也提出状态空间压缩和问题抽象方法[52-53].研究者也尝试对CFR方法的时效性问题和简化问题规模提出解法.王鹏程[54]提出适用于强化学习的模式匹配扑克建模方法,基于蒙特卡罗博弈树搜索计算回报函数,利用基于长短时记忆网络的DQN学习特征,降低了博弈问题求解难度.在非完全信息条件下,基于CFR方法的智能体在决策时建模对手可能采取的所有行动,将其表示为一个信息集,并学习使信息集遗憾值最小的自身策略. ...
... [51]将平均策略的收益加以衰减,提高了近期迭代策略的权重.针对CFR算法的存储效率问题,研究者们也提出状态空间压缩和问题抽象方法[52-53].研究者也尝试对CFR方法的时效性问题和简化问题规模提出解法.王鹏程[54]提出适用于强化学习的模式匹配扑克建模方法,基于蒙特卡罗博弈树搜索计算回报函数,利用基于长短时记忆网络的DQN学习特征,降低了博弈问题求解难度.在非完全信息条件下,基于CFR方法的智能体在决策时建模对手可能采取的所有行动,将其表示为一个信息集,并学习使信息集遗憾值最小的自身策略. ...
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
Better Automated Abstraction Techniques for Imperfect Information Games, with Application to Texas Hold'em Poker
1
2007
... 为解决最小化反事实遗憾值方法计算速度问题,研究者们从其原理出发提出一系列在线学习方法[47-51].Lanctot等[48]采用蒙特卡罗采样方式对博弈树进行部分抽样,相较原方法计算效率提升10倍,并且证明抽样更新的遗憾收益值是真实值的无偏估计.Tammelin[51]将平均策略的收益加以衰减,提高了近期迭代策略的权重.针对CFR算法的存储效率问题,研究者们也提出状态空间压缩和问题抽象方法[52-53].研究者也尝试对CFR方法的时效性问题和简化问题规模提出解法.王鹏程[54]提出适用于强化学习的模式匹配扑克建模方法,基于蒙特卡罗博弈树搜索计算回报函数,利用基于长短时记忆网络的DQN学习特征,降低了博弈问题求解难度.在非完全信息条件下,基于CFR方法的智能体在决策时建模对手可能采取的所有行动,将其表示为一个信息集,并学习使信息集遗憾值最小的自身策略. ...
Abstraction Pathologies in Extensive Games
1
2009
... 为解决最小化反事实遗憾值方法计算速度问题,研究者们从其原理出发提出一系列在线学习方法[47-51].Lanctot等[48]采用蒙特卡罗采样方式对博弈树进行部分抽样,相较原方法计算效率提升10倍,并且证明抽样更新的遗憾收益值是真实值的无偏估计.Tammelin[51]将平均策略的收益加以衰减,提高了近期迭代策略的权重.针对CFR算法的存储效率问题,研究者们也提出状态空间压缩和问题抽象方法[52-53].研究者也尝试对CFR方法的时效性问题和简化问题规模提出解法.王鹏程[54]提出适用于强化学习的模式匹配扑克建模方法,基于蒙特卡罗博弈树搜索计算回报函数,利用基于长短时记忆网络的DQN学习特征,降低了博弈问题求解难度.在非完全信息条件下,基于CFR方法的智能体在决策时建模对手可能采取的所有行动,将其表示为一个信息集,并学习使信息集遗憾值最小的自身策略. ...
基于深度强化学习的非完备信息机器博弈研究
1
2016
... 为解决最小化反事实遗憾值方法计算速度问题,研究者们从其原理出发提出一系列在线学习方法[47-51].Lanctot等[48]采用蒙特卡罗采样方式对博弈树进行部分抽样,相较原方法计算效率提升10倍,并且证明抽样更新的遗憾收益值是真实值的无偏估计.Tammelin[51]将平均策略的收益加以衰减,提高了近期迭代策略的权重.针对CFR算法的存储效率问题,研究者们也提出状态空间压缩和问题抽象方法[52-53].研究者也尝试对CFR方法的时效性问题和简化问题规模提出解法.王鹏程[54]提出适用于强化学习的模式匹配扑克建模方法,基于蒙特卡罗博弈树搜索计算回报函数,利用基于长短时记忆网络的DQN学习特征,降低了博弈问题求解难度.在非完全信息条件下,基于CFR方法的智能体在决策时建模对手可能采取的所有行动,将其表示为一个信息集,并学习使信息集遗憾值最小的自身策略. ...
Research on Imperfect Information Machine Game Based on Deep Reinforcement Learning
1
2016
... 为解决最小化反事实遗憾值方法计算速度问题,研究者们从其原理出发提出一系列在线学习方法[47-51].Lanctot等[48]采用蒙特卡罗采样方式对博弈树进行部分抽样,相较原方法计算效率提升10倍,并且证明抽样更新的遗憾收益值是真实值的无偏估计.Tammelin[51]将平均策略的收益加以衰减,提高了近期迭代策略的权重.针对CFR算法的存储效率问题,研究者们也提出状态空间压缩和问题抽象方法[52-53].研究者也尝试对CFR方法的时效性问题和简化问题规模提出解法.王鹏程[54]提出适用于强化学习的模式匹配扑克建模方法,基于蒙特卡罗博弈树搜索计算回报函数,利用基于长短时记忆网络的DQN学习特征,降低了博弈问题求解难度.在非完全信息条件下,基于CFR方法的智能体在决策时建模对手可能采取的所有行动,将其表示为一个信息集,并学习使信息集遗憾值最小的自身策略. ...
Level-0 Models for Predicting Human Behavior in Games
2
2019
... 上述两类模型是从纳什均衡角度求解对手建模的最优策略,而MiniMax均衡是以安全性为前提的均衡策略对手建模方法.Wright等[55]改进了定量认知层次模型中的0级(Level-0)模型,首先手工筛选出最大最小收益、最小最大悔度等特征,将这些特征线性加权组合成为0级模型以表示智能体的初始行为,再将0级模型经过定量认知推理后得到一个有限层次推理的对手行为模型.该方法在多种游戏的玩家数据集中实验,测试结果表明对手建模能够模拟出有限程度理性的人类行为. ...
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
Robust Multi-agent Reinforcement Learning via Minimax Deep Deterministic Policy Gradient
4
2019
... Li等[56]将最大最小思想作为多智能体环境中鲁棒学习的一种方法,即使智能体在训练中没有获得最优策略,学习到的鲁棒策略也使任务表现足够良好.徐浩添将MADDPG算法[57]扩展到最大最小多智能体深度确定性策略梯度(minimax multi-agent deep deterministic policy gradient, M3DDPG)[56],该算法在考虑最坏情况的假设下更新策略,即对手模型假设所有其他智能体都将采取敌对行动,并且选择能够使自身收益最小的策略.最大最小策略的学习目标在连续动作空间计算上难以直接优化,因此,他们通过鲁棒强化学习中的最差噪声概念隐含地学习最大最小值,提出了多智能体对抗学习来解决计算最大最小策略的问题. ...
... [56],该算法在考虑最坏情况的假设下更新策略,即对手模型假设所有其他智能体都将采取敌对行动,并且选择能够使自身收益最小的策略.最大最小策略的学习目标在连续动作空间计算上难以直接优化,因此,他们通过鲁棒强化学习中的最差噪声概念隐含地学习最大最小值,提出了多智能体对抗学习来解决计算最大最小策略的问题. ...
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Multi-agent Actor-critic for Mixed Cooperative-competitive Environments
2
2017
... Li等[56]将最大最小思想作为多智能体环境中鲁棒学习的一种方法,即使智能体在训练中没有获得最优策略,学习到的鲁棒策略也使任务表现足够良好.徐浩添将MADDPG算法[57]扩展到最大最小多智能体深度确定性策略梯度(minimax multi-agent deep deterministic policy gradient, M3DDPG)[56],该算法在考虑最坏情况的假设下更新策略,即对手模型假设所有其他智能体都将采取敌对行动,并且选择能够使自身收益最小的策略.最大最小策略的学习目标在连续动作空间计算上难以直接优化,因此,他们通过鲁棒强化学习中的最差噪声概念隐含地学习最大最小值,提出了多智能体对抗学习来解决计算最大最小策略的问题. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Planning in the Presence of Cost Functions Controlled by an Adversary
2
2003
... Research motivation, solved problem and effects of game equilibrium strategy methods
Table 2| 分类 | 方法 | 研究动机 | 对手模型 | 模型效果 |
|---|
| 虚拟 自博弈 | FSP[38] | 将FP推广至扩展式博弈 | 对手的历史平均最佳响应 | 强化学习实现最优响应,监督学习实现平均策略,收敛至纳什均衡 |
| NFSP[39] | 使用神经网络近似最优策略和平均策略 | 多层神经网络近似的对手历史平均最佳响应 | 基于DQN实现端到端学习,并收敛至纳什均衡 |
| PSRO[42] | 求解子博弈元策略,合并成完整策略 | 将博弈对手的历史策略记录在元策略集 | 使用DO算法[58]训练新策略,收敛性受到对手策略采样方式的影响 |
| -PSRO[44] | 训练改进群体的每种策略,而非单纯训练纳什均衡策略 | 马尔科夫-康尼链评价对手种群的质量 | 策略收敛于-rank解[43],改进了群体博弈的均衡收敛性 |
| 反事实 遗憾值 最小化 | MCCFR[48] | 采用蒙特卡罗抽样代替树节点遍历计算各个状态的遗憾值 | 包含对手所有可能行动的信息集 | 蒙特卡罗抽样是对遗憾值无偏估计,且在不完美信息扩展式博弈中快速收敛 |
| CFR+[51] | 采用保证动作的遗憾值为正数,累计值不减少的遗憾值匹配方法 | 包含对手所有可能行动的信息集 | 改进遗憾值匹配机制,使CFR算法加速收敛近似纳什均衡 |
| MiniMax 均衡 | Level-0[55] | 有限理性的对手行动源自0级策略的递归推理,0级策略采用人工筛选策略 | 以MiniMax策略为0级的定量认知层次策略 | 0级策略改进认知层次模型的效果,数据集实验结果有效预测人类行为 |
| M3DDPG[56] | 采用保底策略鲁棒应对变化对手的多智能体DRL算法 | 导致自身收益最小的对手策略 | 采用对抗学习方法求解连续动态环境的MiniMax均衡策略 |
2.2 递归推理建模基于递归推理方法从认知心理学角度刻画了智能体和其他个体的心理活动,试图模仿人类社会的信念推理、意图推理等认知行为过程,期望实现智能体的有限理性决策.主要方法有:①基于心智理论的建模方法;②基于认知层次结构的建模方法;③基于贝叶斯策略复用的建模方法. ...
... 针对交通网络问题,Zhang等[98]提出了在道路网络中封锁犯罪分子逃逸路线的研究,设计一种封锁道路的攻击者-防御者安全博弈模型,并结合基于混合整数线性规划公式的最佳响应和基于高效双Oracle算法[58]的有效近似来计算最佳的防御策略.Xue等[99]将NFSP模型运用在大规模扩展式的网络安防博弈(network security games, NSGs)中,并使用斯坦伯格博弈的形式求解.首先,模型将NFSP中的最佳响应策略网络从行动-状态改造为行动-价值的映射,使NSGs中最佳响应的计算成为可能.随后,将NFSP智能体的平均策略网络转换为基于度量的分类器,为智能体提供高水平的行动,通过学习高效的图节点嵌入来利用NSGs图中包含的信息,模型在可扩展性和质量方面都有显著提升. ...
Theory of Mind
1
2001
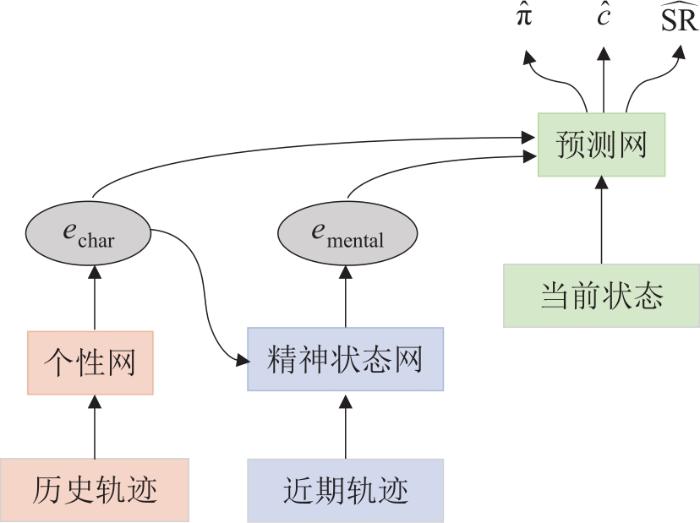
... 心智理论是递归推理中的一类方法[59],被认为是有助于增强深度强化学习可解释性的理论之一.在心智理论方法中,智能体对其他智能体的心理状态有明确的信念.换而言之,其他智能体的心理状态也可能包含该智能体的信念和心理状态.Rabinowitz等[60]根据心智理论提出预测对手特征和精神状态的心智理论网络(theory of mind network, ToMnet).ToMnet通过观察获取对手的先验知识,通过元学习建立智能体的模型.ToMnet遵循一个前提假设:当遇到一个新对手时,智能体应该已经对其行为有了强大且丰富的先验知识. ...
Machine Theory of Mind
2
2018
... 心智理论是递归推理中的一类方法[59],被认为是有助于增强深度强化学习可解释性的理论之一.在心智理论方法中,智能体对其他智能体的心理状态有明确的信念.换而言之,其他智能体的心理状态也可能包含该智能体的信念和心理状态.Rabinowitz等[60]根据心智理论提出预测对手特征和精神状态的心智理论网络(theory of mind network, ToMnet).ToMnet通过观察获取对手的先验知识,通过元学习建立智能体的模型.ToMnet遵循一个前提假设:当遇到一个新对手时,智能体应该已经对其行为有了强大且丰富的先验知识. ...
... Summary of research motivations, innovations and limitations of recursive reasoning methods
Table 3| 类别 | 算法 | 研究动机 | 模型用途 | 创新点 | 局限性 |
|---|
| 心智理论 | ToMnet[60] | 从心智理论提出符合人类认知的元学习对手模型 | 预测的对手行为、目标、信念 | 建立元学习的先验模型,用于预测表征和心智状态 | 适用的实验场景简单,环境完全可观 |
| 认知层次结构 | PR2[63] | 智能体具有推断对手策略的信念递归推理能力 | 推理对手下一步意图 | 提出多智能体概率递归推理的分布式框架,利用变分贝叶斯推理对手策略 | 二人博弈场景收敛,复杂合作场景中表现不足 |
| GR2[64] | 借助不同层次结构的递归推理建模对手的有限理性 | 以K层深度推理对手的下一步意图 | 设计了基于概率图模型的层次结构,并证明存在完美贝叶斯均衡 | 具有递归推理层级选择问题,带来更高计算要求 |
| 贝叶斯 策略复用 | DPN-BPR+[68] | 针对非平稳的对手策略,提出策略检测和复用机制 | 根据收益更新对当前对手策略的信念 | 深度神经网络作为BPR+的值函数近似,使用网络蒸馏存储最优响应策略 | 假定对手在固定策略之间切换,无法识别连续演化的对手策略 |
| Deep Bayes ToMop[69] | 将BPR预测能力和心智理论的递归推理能力结合互补 | 在BPR信念基础上多层递归推理 | 具有学习对手演化和应对未知对手策略的能力 | 在线学习新策略的耗时长,无法应对多个对手 |
3 基于DRL的隐式对手建模隐式对手建模方法没有预置形式化的对手,而是按照任务需求利用对手信息,与深度强化学习结合影响自身决策.因此,根据对手模型的作用机理,本文将基于DRL的隐式对手建模主要方法分为:①基于辅助任务的建模方法;②基于学习表征的建模方法;③基于最大化概率推理的建模方法;④基于自我-他人交互的建模方法. ...
Undecidability in Epistemic Planning
1
2013
... 心理学学者认为人类会将自身信念、意图和情绪归因于他人,并且使用推理能力递归地思考他人的想法,称为信念嵌套[61].通过学习其他玩家信念状态的模型进行递归推理,这种信念的嵌套可以表现为“我相信你相信我相信”.量化认知层次结构利用量化响应和有限迭代策略推理反映有限理性的人类行为.假定每个智能体具有有限K级推理深度,Hartford等[62]将正则博弈的收益矩阵编码,构造模拟递归推理的神经网络结构.第1层网络结构是收益矩阵映射到行动向量的对手策略,作为对手模型的0级策略.从0级到K级推理的过程,前几级的策略将作为隐藏向量输入的神经网络,学习一个从隐藏层映射到动作维度的输出函数,用于模拟对手模型当前一级的策略,实现了基于认知层次结构的对手建模.该方法的优点是避免了手动筛选特征,调试了模型参数,但是该方法的架构设计较为初步,只适用于双人游戏且无重复的博弈. ...
Deep Learning for Predicting Human Strategic Behavior
1
2016
... 心理学学者认为人类会将自身信念、意图和情绪归因于他人,并且使用推理能力递归地思考他人的想法,称为信念嵌套[61].通过学习其他玩家信念状态的模型进行递归推理,这种信念的嵌套可以表现为“我相信你相信我相信”.量化认知层次结构利用量化响应和有限迭代策略推理反映有限理性的人类行为.假定每个智能体具有有限K级推理深度,Hartford等[62]将正则博弈的收益矩阵编码,构造模拟递归推理的神经网络结构.第1层网络结构是收益矩阵映射到行动向量的对手策略,作为对手模型的0级策略.从0级到K级推理的过程,前几级的策略将作为隐藏向量输入的神经网络,学习一个从隐藏层映射到动作维度的输出函数,用于模拟对手模型当前一级的策略,实现了基于认知层次结构的对手建模.该方法的优点是避免了手动筛选特征,调试了模型参数,但是该方法的架构设计较为初步,只适用于双人游戏且无重复的博弈. ...
Probabilistic Recursive Reasoning for Multi-agent Reinforcement Learning
3
1901
... Wen等[63]提出概率递归推理(probabilistic recursive reasoning, PR2)框架,考虑对手下一步行动对自身策略可能带来的影响,将对手建模转化为推理对手下一步行动的条件概率,采用变分贝叶斯方法逼近对手的条件策略,使每个智能体找到最优策略,然后改进当前策略,在DQN和DDPG上实现自博弈收敛至纳什均衡. ...
... Summary of research motivations, innovations and limitations of recursive reasoning methods
Table 3| 类别 | 算法 | 研究动机 | 模型用途 | 创新点 | 局限性 |
|---|
| 心智理论 | ToMnet[60] | 从心智理论提出符合人类认知的元学习对手模型 | 预测的对手行为、目标、信念 | 建立元学习的先验模型,用于预测表征和心智状态 | 适用的实验场景简单,环境完全可观 |
| 认知层次结构 | PR2[63] | 智能体具有推断对手策略的信念递归推理能力 | 推理对手下一步意图 | 提出多智能体概率递归推理的分布式框架,利用变分贝叶斯推理对手策略 | 二人博弈场景收敛,复杂合作场景中表现不足 |
| GR2[64] | 借助不同层次结构的递归推理建模对手的有限理性 | 以K层深度推理对手的下一步意图 | 设计了基于概率图模型的层次结构,并证明存在完美贝叶斯均衡 | 具有递归推理层级选择问题,带来更高计算要求 |
| 贝叶斯 策略复用 | DPN-BPR+[68] | 针对非平稳的对手策略,提出策略检测和复用机制 | 根据收益更新对当前对手策略的信念 | 深度神经网络作为BPR+的值函数近似,使用网络蒸馏存储最优响应策略 | 假定对手在固定策略之间切换,无法识别连续演化的对手策略 |
| Deep Bayes ToMop[69] | 将BPR预测能力和心智理论的递归推理能力结合互补 | 在BPR信念基础上多层递归推理 | 具有学习对手演化和应对未知对手策略的能力 | 在线学习新策略的耗时长,无法应对多个对手 |
3 基于DRL的隐式对手建模隐式对手建模方法没有预置形式化的对手,而是按照任务需求利用对手信息,与深度强化学习结合影响自身决策.因此,根据对手模型的作用机理,本文将基于DRL的隐式对手建模主要方法分为:①基于辅助任务的建模方法;②基于学习表征的建模方法;③基于最大化概率推理的建模方法;④基于自我-他人交互的建模方法. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Modelling Bounded Rationality in Multi-agent Interactions by Generalized Recursive Reasoning
4
2020
... 然而PR2的推理层次只有1级,无法满足有限理性建模的需要.因此,为解决深层次推理的问题,Wen等[64]又在概率图模型基础上设计了广义递归推理(generalized recursive reasoning, GR2)框架,将对手下一步行动的推理拓展到了K层级推理,其中第k级推理为对1~k-1级策略联合条件概率的最优响应策略,而对手模型是基于前K-1级策略做出的最优策略.从当前状态s开始,智能体i的1级行为取决于对手0级行动,k级行为取决于对手的k-1级行动提供深层次推理结构的理论支撑.如图4所示,在此基础上推导出GR2演员-评论家算法,理论上证明了GR2条件下完美贝叶斯均衡的存在性,以及策略梯度方法在二人范式博弈上的收敛性. ...
... Summary of research motivations, innovations and limitations of recursive reasoning methods
Table 3| 类别 | 算法 | 研究动机 | 模型用途 | 创新点 | 局限性 |
|---|
| 心智理论 | ToMnet[60] | 从心智理论提出符合人类认知的元学习对手模型 | 预测的对手行为、目标、信念 | 建立元学习的先验模型,用于预测表征和心智状态 | 适用的实验场景简单,环境完全可观 |
| 认知层次结构 | PR2[63] | 智能体具有推断对手策略的信念递归推理能力 | 推理对手下一步意图 | 提出多智能体概率递归推理的分布式框架,利用变分贝叶斯推理对手策略 | 二人博弈场景收敛,复杂合作场景中表现不足 |
| GR2[64] | 借助不同层次结构的递归推理建模对手的有限理性 | 以K层深度推理对手的下一步意图 | 设计了基于概率图模型的层次结构,并证明存在完美贝叶斯均衡 | 具有递归推理层级选择问题,带来更高计算要求 |
| 贝叶斯 策略复用 | DPN-BPR+[68] | 针对非平稳的对手策略,提出策略检测和复用机制 | 根据收益更新对当前对手策略的信念 | 深度神经网络作为BPR+的值函数近似,使用网络蒸馏存储最优响应策略 | 假定对手在固定策略之间切换,无法识别连续演化的对手策略 |
| Deep Bayes ToMop[69] | 将BPR预测能力和心智理论的递归推理能力结合互补 | 在BPR信念基础上多层递归推理 | 具有学习对手演化和应对未知对手策略的能力 | 在线学习新策略的耗时长,无法应对多个对手 |
3 基于DRL的隐式对手建模隐式对手建模方法没有预置形式化的对手,而是按照任务需求利用对手信息,与深度强化学习结合影响自身决策.因此,根据对手模型的作用机理,本文将基于DRL的隐式对手建模主要方法分为:①基于辅助任务的建模方法;②基于学习表征的建模方法;③基于最大化概率推理的建模方法;④基于自我-他人交互的建模方法. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
... -
64,
116]
部分可观 | 合作 | 同步 | 离散 | | FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Multiagent Deep Reinforcement Learning: Challenges and Directions Towards Human-Like Approaches
1
... 以往的对手建模通常假定智能体执行固定策略,研究者们注意到智能体可能在多种策略间切换选择,因此,设计出监测和学习对手策略的对手建模机制.切换智能体模型是一类结合贝叶斯神经网络,从观察到的状态-动作轨迹中学习对手模型的研究[65].贝叶斯策略重用[66]是一个根据收益更新任务信念的贝叶斯模型,选择最大化收益的策略作为当前最可信的策略. ...
Learning Against Non-stationary Agents with Opponent Modelling and Deep Reinforcement Learning
2
2018
... 以往的对手建模通常假定智能体执行固定策略,研究者们注意到智能体可能在多种策略间切换选择,因此,设计出监测和学习对手策略的对手建模机制.切换智能体模型是一类结合贝叶斯神经网络,从观察到的状态-动作轨迹中学习对手模型的研究[65].贝叶斯策略重用[66]是一个根据收益更新任务信念的贝叶斯模型,选择最大化收益的策略作为当前最可信的策略. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
A Bayesian Approach for Learning and Tracking Switching, Non-stationary opponents
1
2016
... Hernandez等[67]提出改进的贝叶斯策略重用+ ...
A Deep Bayesian Policy Reuse Approach against Non-stationary Agents
3
2018
... (Bayesian policy reuse+ , BPR+)算法,将贝叶斯策略重用框架从单智能体扩展到了多智能体情景,以在线方式学习新的性能模型.BPR+方法的对手模型是一个以奖励评估对手策略信任度的贝叶斯模型,选择当前最可信的策略作为对手策略.然而BPR+的局限性是它的自我博弈行为策略表现不佳.为了提升模型的泛化性,Zheng等[68]提出蒸馏策略网络-贝叶斯策略重用+(distilled policy network-Bayesian policy reuse+, DPN-BPR+),通过神经网络扩展了BPR+算法,并且根据行为和奖励信号共同检测对手策略.然而上述方法没有考虑具有复杂决策逻辑的对手策略识别问题,Yang等[69]从贝叶斯心智理论获得灵感,提出一种深度贝叶斯心智方法(deep Bayesian theory of mind, Deep Bayes-ToMoP)用于识别高层次推理策略,考虑策略库中对手策略的信任度以应对不同类型智能体.Deep Bayes-ToMoP根据心智理论的递归推理框架提供了一个更高层次的推理策略,识别应对未知的对手策略,面对复杂的决策逻辑也能获得智能体的最优对策. ...
... Summary of research motivations, innovations and limitations of recursive reasoning methods
Table 3| 类别 | 算法 | 研究动机 | 模型用途 | 创新点 | 局限性 |
|---|
| 心智理论 | ToMnet[60] | 从心智理论提出符合人类认知的元学习对手模型 | 预测的对手行为、目标、信念 | 建立元学习的先验模型,用于预测表征和心智状态 | 适用的实验场景简单,环境完全可观 |
| 认知层次结构 | PR2[63] | 智能体具有推断对手策略的信念递归推理能力 | 推理对手下一步意图 | 提出多智能体概率递归推理的分布式框架,利用变分贝叶斯推理对手策略 | 二人博弈场景收敛,复杂合作场景中表现不足 |
| GR2[64] | 借助不同层次结构的递归推理建模对手的有限理性 | 以K层深度推理对手的下一步意图 | 设计了基于概率图模型的层次结构,并证明存在完美贝叶斯均衡 | 具有递归推理层级选择问题,带来更高计算要求 |
| 贝叶斯 策略复用 | DPN-BPR+[68] | 针对非平稳的对手策略,提出策略检测和复用机制 | 根据收益更新对当前对手策略的信念 | 深度神经网络作为BPR+的值函数近似,使用网络蒸馏存储最优响应策略 | 假定对手在固定策略之间切换,无法识别连续演化的对手策略 |
| Deep Bayes ToMop[69] | 将BPR预测能力和心智理论的递归推理能力结合互补 | 在BPR信念基础上多层递归推理 | 具有学习对手演化和应对未知对手策略的能力 | 在线学习新策略的耗时长,无法应对多个对手 |
3 基于DRL的隐式对手建模隐式对手建模方法没有预置形式化的对手,而是按照任务需求利用对手信息,与深度强化学习结合影响自身决策.因此,根据对手模型的作用机理,本文将基于DRL的隐式对手建模主要方法分为:①基于辅助任务的建模方法;②基于学习表征的建模方法;③基于最大化概率推理的建模方法;④基于自我-他人交互的建模方法. ...
... 针对单个网络模型对策略表示能力不足的问题,Shen等[115]在学习对手策略时采用集成学习方法[139]训练多个网络共同表示当前对手模型,提高了模型的鲁棒性.除了集成学习思想,知识蒸馏也是提高模型准确性的一种方法[140].知识蒸馏综合了多种专家网络,压缩网络结构信息,保留学习到的知识,经过知识蒸馏后的对手策略模型仍然保留了网络的对手特征提取能力[68,115]. ...
Towards Efficient Detection and Optimal Response Against Sophisticated Opponents
3
2019
... (Bayesian policy reuse+ , BPR+)算法,将贝叶斯策略重用框架从单智能体扩展到了多智能体情景,以在线方式学习新的性能模型.BPR+方法的对手模型是一个以奖励评估对手策略信任度的贝叶斯模型,选择当前最可信的策略作为对手策略.然而BPR+的局限性是它的自我博弈行为策略表现不佳.为了提升模型的泛化性,Zheng等[68]提出蒸馏策略网络-贝叶斯策略重用+(distilled policy network-Bayesian policy reuse+, DPN-BPR+),通过神经网络扩展了BPR+算法,并且根据行为和奖励信号共同检测对手策略.然而上述方法没有考虑具有复杂决策逻辑的对手策略识别问题,Yang等[69]从贝叶斯心智理论获得灵感,提出一种深度贝叶斯心智方法(deep Bayesian theory of mind, Deep Bayes-ToMoP)用于识别高层次推理策略,考虑策略库中对手策略的信任度以应对不同类型智能体.Deep Bayes-ToMoP根据心智理论的递归推理框架提供了一个更高层次的推理策略,识别应对未知的对手策略,面对复杂的决策逻辑也能获得智能体的最优对策. ...
... Summary of research motivations, innovations and limitations of recursive reasoning methods
Table 3| 类别 | 算法 | 研究动机 | 模型用途 | 创新点 | 局限性 |
|---|
| 心智理论 | ToMnet[60] | 从心智理论提出符合人类认知的元学习对手模型 | 预测的对手行为、目标、信念 | 建立元学习的先验模型,用于预测表征和心智状态 | 适用的实验场景简单,环境完全可观 |
| 认知层次结构 | PR2[63] | 智能体具有推断对手策略的信念递归推理能力 | 推理对手下一步意图 | 提出多智能体概率递归推理的分布式框架,利用变分贝叶斯推理对手策略 | 二人博弈场景收敛,复杂合作场景中表现不足 |
| GR2[64] | 借助不同层次结构的递归推理建模对手的有限理性 | 以K层深度推理对手的下一步意图 | 设计了基于概率图模型的层次结构,并证明存在完美贝叶斯均衡 | 具有递归推理层级选择问题,带来更高计算要求 |
| 贝叶斯 策略复用 | DPN-BPR+[68] | 针对非平稳的对手策略,提出策略检测和复用机制 | 根据收益更新对当前对手策略的信念 | 深度神经网络作为BPR+的值函数近似,使用网络蒸馏存储最优响应策略 | 假定对手在固定策略之间切换,无法识别连续演化的对手策略 |
| Deep Bayes ToMop[69] | 将BPR预测能力和心智理论的递归推理能力结合互补 | 在BPR信念基础上多层递归推理 | 具有学习对手演化和应对未知对手策略的能力 | 在线学习新策略的耗时长,无法应对多个对手 |
3 基于DRL的隐式对手建模隐式对手建模方法没有预置形式化的对手,而是按照任务需求利用对手信息,与深度强化学习结合影响自身决策.因此,根据对手模型的作用机理,本文将基于DRL的隐式对手建模主要方法分为:①基于辅助任务的建模方法;②基于学习表征的建模方法;③基于最大化概率推理的建模方法;④基于自我-他人交互的建模方法. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Playing FPS Games with Deep Reinforcement Learning
1
2017
... 辅助任务是一种多任务的DRL方法[70],为智能体提供了更丰富的行为动机,适合非平稳环境的学习任务.辅助任务的建模方法设计获取对手特征的模型,修正强化学习的策略和价值函数,为强化学习提供与对手博弈的行为动机.该方法将其他智能体的观测编码作为监督信息输入神经网络进行训练,提取对手策略特征,用于修正强化学习的策略和价值函数,完成最大化奖励的目标[26,71-72].这类方法中具有开创性的工作是He等[26]提出的深度强化对手网络(deep reinforcement opponent network, DRON).在多智能体系统中,对手的行动将会改变环境状态转移,从而影响智能体强化学习过程的收敛性.因此,DRON同时训练Q值网络和对手策略表征网络,将对手策略表征作为环境已知条件帮助Q值网络收敛.在具体实现中,DRON在DQN的基础上改造,使用一个网络评估Q值,另一个网络则负责对手建模,以对手的行动作为输入,捕获当前对手的特征,用于学习对手策略.在此基础上,它结合多个专家网络预测估计Q值,每个专家网络捕获一种对手策略.在1v1足球比赛场景下DRON智能体与基于规则的对手智能体对抗训练,DRON智能体赢得了99.86%的进攻,并且防守成功不低于90.20%.该方法的缺点是专家网络的模型和输入需要依据先验知识手工设定. ...
A Deep Policy Inference Q-Network for Multi-agent Systems
5
2018
... 辅助任务是一种多任务的DRL方法[70],为智能体提供了更丰富的行为动机,适合非平稳环境的学习任务.辅助任务的建模方法设计获取对手特征的模型,修正强化学习的策略和价值函数,为强化学习提供与对手博弈的行为动机.该方法将其他智能体的观测编码作为监督信息输入神经网络进行训练,提取对手策略特征,用于修正强化学习的策略和价值函数,完成最大化奖励的目标[26,71-72].这类方法中具有开创性的工作是He等[26]提出的深度强化对手网络(deep reinforcement opponent network, DRON).在多智能体系统中,对手的行动将会改变环境状态转移,从而影响智能体强化学习过程的收敛性.因此,DRON同时训练Q值网络和对手策略表征网络,将对手策略表征作为环境已知条件帮助Q值网络收敛.在具体实现中,DRON在DQN的基础上改造,使用一个网络评估Q值,另一个网络则负责对手建模,以对手的行动作为输入,捕获当前对手的特征,用于学习对手策略.在此基础上,它结合多个专家网络预测估计Q值,每个专家网络捕获一种对手策略.在1v1足球比赛场景下DRON智能体与基于规则的对手智能体对抗训练,DRON智能体赢得了99.86%的进攻,并且防守成功不低于90.20%.该方法的缺点是专家网络的模型和输入需要依据先验知识手工设定. ...
... 与人工方法相比,许多研究采用监督学习的方法选取特征.例如,深度策略推理Q网络(deep policy inference Q-network, DPIQN)[71]和深度策略推理循环Q网络(deep policy inference recurrent Q-network, DPIRQN)[71]计算推断出对手策略和对手的真实观察(one-hot编码的动作向量)之间的交叉熵,提出一种自适应系数辅助修正对手模型的损失函数,用于学习对手策略的辅助任务.DPIQN和DPIRQN通过卷积神经网络处理图像数据后,将隐藏层向量分别输入Q值网络和策略特征学习网络中.策略特征学习网络是一个多层感知机或LSTM网络,用于从隐藏向量提取对手策略特征,分别用于Q学习任务和还原对手策略的辅助任务,并根据任务损失修正网络.同样在1v1足球场景中,DPIQN智能体几乎完全赢得与基于规则对手的比赛.此外,Hernandez-Leal等[72]在A3C算法的基础上实现参数共享对手建模(agent modeling by parameter sharing, AMS).AMS-A3C算法基于一套共享的A3C神经网络结构决策和建模对手,利用修正的损失函数完成改进自身策略的强化学习任务和监督学习拟合对手行动策略的辅助任务.实验测试中,利用CNN网络从像素游戏画面提取对手的隐含特征,用于学习预测对手策略的辅助任务网络. ...
... [71]计算推断出对手策略和对手的真实观察(one-hot编码的动作向量)之间的交叉熵,提出一种自适应系数辅助修正对手模型的损失函数,用于学习对手策略的辅助任务.DPIQN和DPIRQN通过卷积神经网络处理图像数据后,将隐藏层向量分别输入Q值网络和策略特征学习网络中.策略特征学习网络是一个多层感知机或LSTM网络,用于从隐藏向量提取对手策略特征,分别用于Q学习任务和还原对手策略的辅助任务,并根据任务损失修正网络.同样在1v1足球场景中,DPIQN智能体几乎完全赢得与基于规则对手的比赛.此外,Hernandez-Leal等[72]在A3C算法的基础上实现参数共享对手建模(agent modeling by parameter sharing, AMS).AMS-A3C算法基于一套共享的A3C神经网络结构决策和建模对手,利用修正的损失函数完成改进自身策略的强化学习任务和监督学习拟合对手行动策略的辅助任务.实验测试中,利用CNN网络从像素游戏画面提取对手的隐含特征,用于学习预测对手策略的辅助任务网络. ...
... Summary of research motivation, innovation points and limitations of implicit based opponent modeling methods
Table 4| 类别 | 算法 | 研究动机 | 模型特点 | 创新点 | 局限性 |
|---|
| 辅助 任务 | DRON[26] | 设计挖掘不同对手策略隐藏特征的神经网络 | 使用MLP处理对手行动,将表征信息用于强化学习任务 | 提取对手特征用于DRL算法决策 | 手工提取输入专家网络的特征,可采用RNN改进 |
| DIPQN[71] | 从观测直接提取对手策略特征,训练对手建模的辅助任务 | 策略特征网络学习从观测提取表征,并通过行为克隆的准确性修正网络 | 设计了调节最大奖励与对手建模的自适应损失函数 | 采用经验回放池离线训练,学习的对手策略具有较大样本方差 |
| AMS-A3C[72] | 在强化学习过程中,制订估计其他智能体策略的辅助任务 | 决策网络与模仿决策的对手模型共享结构、参数,降低模型学习成本 | 提出参数共享、策略表征2套方案,将对手建模融合进A3C算法 | 对手模型参数敏感,难以应对复杂场景、具有学习能力的对手 |
| 学习 表征 | PPO-Emb[74] | 从交互样本中无监督地学习对手表征 | 提取同时具有策略提升效果和对手区分度的表征信息 | 无需领域知识,通用性强,适用大多数DRL算法 | 无法独立推断,用于辅助其他DRL算法决策 |
| RFM[73] | 采用图网络学习智能体的社会关系表征 | 通过边缘属性、节点等图结构信息预测对手行动、评估对手社会关系强度 | 量化智能体交互的社会属性,网络结构具有较好拓展性 | 存在复杂交互关系的图网络计算困难 |
| 概率 推理 | P-BIT[76] | 多智能体DRL的最优策略形式化为推理私有信息的概率下界 | 使用信念模块根据友方行为推理其私有信息 | 提出不完美信息条件下通过行动与队友传递私有信息的方法 | 适用于简单的二人合作场景 |
| ROMMEO[78] | 多智能体DRL形式化为基于对手模型的最优策略变分推理 | 预测对手行动,用于实现学习最优策略的推理任务 | 提出最大熵目标的正则化的对手建模方法 | 在线优化参数,训练时间长.默认对手目标已知,无法适应未知智能体 |
| 自我- 他人交互 | SOM[79] | 基于自身策略推理对手可能的目标,用于支撑决策 | 建立拟合对手策略的神经网络,通过优化对手策略反向推断对手的目标 | 无需额外模型和参数显式建模,仿照自身模型推理任意数量规模对手 | 智能体与对手共享目标,并且奖励结构取决于目标 |
| LOLA[81] | 考虑具有学习能力的对手,解释对手学习参数的更新对自身策略影响 | 建模对手的价值函数,求其二阶导优化策略梯度 | 策略更新中增加了对手参数更新项,通过泰勒展开构造成高阶梯度项 | 默认对手使用可梯度优化的方法,并且无法察觉LOLA对其模型进行利用 |
4 应用场景DRL-OM方法起初应用于游戏领域的智能体建模,随着深度强化学习算法在现实场景中的落地应用,DRL-OM技术也拓展到军事仿真、公共安全等诸多领域. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Agent Modeling as Auxiliary Task for Deep Reinforcement Learning
4
2019
... 辅助任务是一种多任务的DRL方法[70],为智能体提供了更丰富的行为动机,适合非平稳环境的学习任务.辅助任务的建模方法设计获取对手特征的模型,修正强化学习的策略和价值函数,为强化学习提供与对手博弈的行为动机.该方法将其他智能体的观测编码作为监督信息输入神经网络进行训练,提取对手策略特征,用于修正强化学习的策略和价值函数,完成最大化奖励的目标[26,71-72].这类方法中具有开创性的工作是He等[26]提出的深度强化对手网络(deep reinforcement opponent network, DRON).在多智能体系统中,对手的行动将会改变环境状态转移,从而影响智能体强化学习过程的收敛性.因此,DRON同时训练Q值网络和对手策略表征网络,将对手策略表征作为环境已知条件帮助Q值网络收敛.在具体实现中,DRON在DQN的基础上改造,使用一个网络评估Q值,另一个网络则负责对手建模,以对手的行动作为输入,捕获当前对手的特征,用于学习对手策略.在此基础上,它结合多个专家网络预测估计Q值,每个专家网络捕获一种对手策略.在1v1足球比赛场景下DRON智能体与基于规则的对手智能体对抗训练,DRON智能体赢得了99.86%的进攻,并且防守成功不低于90.20%.该方法的缺点是专家网络的模型和输入需要依据先验知识手工设定. ...
... 与人工方法相比,许多研究采用监督学习的方法选取特征.例如,深度策略推理Q网络(deep policy inference Q-network, DPIQN)[71]和深度策略推理循环Q网络(deep policy inference recurrent Q-network, DPIRQN)[71]计算推断出对手策略和对手的真实观察(one-hot编码的动作向量)之间的交叉熵,提出一种自适应系数辅助修正对手模型的损失函数,用于学习对手策略的辅助任务.DPIQN和DPIRQN通过卷积神经网络处理图像数据后,将隐藏层向量分别输入Q值网络和策略特征学习网络中.策略特征学习网络是一个多层感知机或LSTM网络,用于从隐藏向量提取对手策略特征,分别用于Q学习任务和还原对手策略的辅助任务,并根据任务损失修正网络.同样在1v1足球场景中,DPIQN智能体几乎完全赢得与基于规则对手的比赛.此外,Hernandez-Leal等[72]在A3C算法的基础上实现参数共享对手建模(agent modeling by parameter sharing, AMS).AMS-A3C算法基于一套共享的A3C神经网络结构决策和建模对手,利用修正的损失函数完成改进自身策略的强化学习任务和监督学习拟合对手行动策略的辅助任务.实验测试中,利用CNN网络从像素游戏画面提取对手的隐含特征,用于学习预测对手策略的辅助任务网络. ...
... Summary of research motivation, innovation points and limitations of implicit based opponent modeling methods
Table 4| 类别 | 算法 | 研究动机 | 模型特点 | 创新点 | 局限性 |
|---|
| 辅助 任务 | DRON[26] | 设计挖掘不同对手策略隐藏特征的神经网络 | 使用MLP处理对手行动,将表征信息用于强化学习任务 | 提取对手特征用于DRL算法决策 | 手工提取输入专家网络的特征,可采用RNN改进 |
| DIPQN[71] | 从观测直接提取对手策略特征,训练对手建模的辅助任务 | 策略特征网络学习从观测提取表征,并通过行为克隆的准确性修正网络 | 设计了调节最大奖励与对手建模的自适应损失函数 | 采用经验回放池离线训练,学习的对手策略具有较大样本方差 |
| AMS-A3C[72] | 在强化学习过程中,制订估计其他智能体策略的辅助任务 | 决策网络与模仿决策的对手模型共享结构、参数,降低模型学习成本 | 提出参数共享、策略表征2套方案,将对手建模融合进A3C算法 | 对手模型参数敏感,难以应对复杂场景、具有学习能力的对手 |
| 学习 表征 | PPO-Emb[74] | 从交互样本中无监督地学习对手表征 | 提取同时具有策略提升效果和对手区分度的表征信息 | 无需领域知识,通用性强,适用大多数DRL算法 | 无法独立推断,用于辅助其他DRL算法决策 |
| RFM[73] | 采用图网络学习智能体的社会关系表征 | 通过边缘属性、节点等图结构信息预测对手行动、评估对手社会关系强度 | 量化智能体交互的社会属性,网络结构具有较好拓展性 | 存在复杂交互关系的图网络计算困难 |
| 概率 推理 | P-BIT[76] | 多智能体DRL的最优策略形式化为推理私有信息的概率下界 | 使用信念模块根据友方行为推理其私有信息 | 提出不完美信息条件下通过行动与队友传递私有信息的方法 | 适用于简单的二人合作场景 |
| ROMMEO[78] | 多智能体DRL形式化为基于对手模型的最优策略变分推理 | 预测对手行动,用于实现学习最优策略的推理任务 | 提出最大熵目标的正则化的对手建模方法 | 在线优化参数,训练时间长.默认对手目标已知,无法适应未知智能体 |
| 自我- 他人交互 | SOM[79] | 基于自身策略推理对手可能的目标,用于支撑决策 | 建立拟合对手策略的神经网络,通过优化对手策略反向推断对手的目标 | 无需额外模型和参数显式建模,仿照自身模型推理任意数量规模对手 | 智能体与对手共享目标,并且奖励结构取决于目标 |
| LOLA[81] | 考虑具有学习能力的对手,解释对手学习参数的更新对自身策略影响 | 建模对手的价值函数,求其二阶导优化策略梯度 | 策略更新中增加了对手参数更新项,通过泰勒展开构造成高阶梯度项 | 默认对手使用可梯度优化的方法,并且无法察觉LOLA对其模型进行利用 |
4 应用场景DRL-OM方法起初应用于游戏领域的智能体建模,随着深度强化学习算法在现实场景中的落地应用,DRL-OM技术也拓展到军事仿真、公共安全等诸多领域. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Relational Forward Models for Multi-agent Learning
3
1809
... 学习表征的建模方法以无监督的学习形式从观测信息中提取对手的表征信息,用于增强深度学习网络的输入信息,无需数据集、奖励等先验知识,提取表征的常见结构包括图神经网络架构[73]、前馈神经网络[74]、循环神经网络[75]等. ...
... Tacchetti等[73]提出基于图神经网络表征的关系前向模型(relational forward models, RFM),以环境中的对手收益作为监督信号,训练图网络在输入环境描述后,准确预测出对手的未来行为和奖励,并增强优势演员-评论家方法的表现.RFM模型是由图、边缘、节点及各自属性构成的图神经模型,其中产生的中间表征可以分析多智能体系统的社会属性,如边缘属性的大小能够解释对手采取行动的幅度,增删节点后计算边际奖励来衡量对手的社会关系强度和效用.此外,图神经网络表征具有很强的关系表示能力,具有网络拓展性,能够和RNN等神经网络结构结合. ...
... Summary of research motivation, innovation points and limitations of implicit based opponent modeling methods
Table 4| 类别 | 算法 | 研究动机 | 模型特点 | 创新点 | 局限性 |
|---|
| 辅助 任务 | DRON[26] | 设计挖掘不同对手策略隐藏特征的神经网络 | 使用MLP处理对手行动,将表征信息用于强化学习任务 | 提取对手特征用于DRL算法决策 | 手工提取输入专家网络的特征,可采用RNN改进 |
| DIPQN[71] | 从观测直接提取对手策略特征,训练对手建模的辅助任务 | 策略特征网络学习从观测提取表征,并通过行为克隆的准确性修正网络 | 设计了调节最大奖励与对手建模的自适应损失函数 | 采用经验回放池离线训练,学习的对手策略具有较大样本方差 |
| AMS-A3C[72] | 在强化学习过程中,制订估计其他智能体策略的辅助任务 | 决策网络与模仿决策的对手模型共享结构、参数,降低模型学习成本 | 提出参数共享、策略表征2套方案,将对手建模融合进A3C算法 | 对手模型参数敏感,难以应对复杂场景、具有学习能力的对手 |
| 学习 表征 | PPO-Emb[74] | 从交互样本中无监督地学习对手表征 | 提取同时具有策略提升效果和对手区分度的表征信息 | 无需领域知识,通用性强,适用大多数DRL算法 | 无法独立推断,用于辅助其他DRL算法决策 |
| RFM[73] | 采用图网络学习智能体的社会关系表征 | 通过边缘属性、节点等图结构信息预测对手行动、评估对手社会关系强度 | 量化智能体交互的社会属性,网络结构具有较好拓展性 | 存在复杂交互关系的图网络计算困难 |
| 概率 推理 | P-BIT[76] | 多智能体DRL的最优策略形式化为推理私有信息的概率下界 | 使用信念模块根据友方行为推理其私有信息 | 提出不完美信息条件下通过行动与队友传递私有信息的方法 | 适用于简单的二人合作场景 |
| ROMMEO[78] | 多智能体DRL形式化为基于对手模型的最优策略变分推理 | 预测对手行动,用于实现学习最优策略的推理任务 | 提出最大熵目标的正则化的对手建模方法 | 在线优化参数,训练时间长.默认对手目标已知,无法适应未知智能体 |
| 自我- 他人交互 | SOM[79] | 基于自身策略推理对手可能的目标,用于支撑决策 | 建立拟合对手策略的神经网络,通过优化对手策略反向推断对手的目标 | 无需额外模型和参数显式建模,仿照自身模型推理任意数量规模对手 | 智能体与对手共享目标,并且奖励结构取决于目标 |
| LOLA[81] | 考虑具有学习能力的对手,解释对手学习参数的更新对自身策略影响 | 建模对手的价值函数,求其二阶导优化策略梯度 | 策略更新中增加了对手参数更新项,通过泰勒展开构造成高阶梯度项 | 默认对手使用可梯度优化的方法,并且无法察觉LOLA对其模型进行利用 |
4 应用场景DRL-OM方法起初应用于游戏领域的智能体建模,随着深度强化学习算法在现实场景中的落地应用,DRL-OM技术也拓展到军事仿真、公共安全等诸多领域. ...
Learning Policy Representations in Multiagent Systems
3
2018
... 学习表征的建模方法以无监督的学习形式从观测信息中提取对手的表征信息,用于增强深度学习网络的输入信息,无需数据集、奖励等先验知识,提取表征的常见结构包括图神经网络架构[73]、前馈神经网络[74]、循环神经网络[75]等. ...
... Grover等[74]从设计优化损失函数的角度提出一种基于前馈神经网络的对手表征学习框架“Emb”,设计了一种基于编码器-解码器的无监督学习结构.根据不同策略对手表征的真实性和差异性设计损失函数,从与对手交互的历史数据中学习连续表征.随后,在PPO算法的基础上实现具有表征增强的PPO-Emb方法,验证了对手表征对强化学习策略的提升效果.Emb框架的优点是采用无监督学习对手特征,样本利用高效,无需任务领域知识. ...
... Summary of research motivation, innovation points and limitations of implicit based opponent modeling methods
Table 4| 类别 | 算法 | 研究动机 | 模型特点 | 创新点 | 局限性 |
|---|
| 辅助 任务 | DRON[26] | 设计挖掘不同对手策略隐藏特征的神经网络 | 使用MLP处理对手行动,将表征信息用于强化学习任务 | 提取对手特征用于DRL算法决策 | 手工提取输入专家网络的特征,可采用RNN改进 |
| DIPQN[71] | 从观测直接提取对手策略特征,训练对手建模的辅助任务 | 策略特征网络学习从观测提取表征,并通过行为克隆的准确性修正网络 | 设计了调节最大奖励与对手建模的自适应损失函数 | 采用经验回放池离线训练,学习的对手策略具有较大样本方差 |
| AMS-A3C[72] | 在强化学习过程中,制订估计其他智能体策略的辅助任务 | 决策网络与模仿决策的对手模型共享结构、参数,降低模型学习成本 | 提出参数共享、策略表征2套方案,将对手建模融合进A3C算法 | 对手模型参数敏感,难以应对复杂场景、具有学习能力的对手 |
| 学习 表征 | PPO-Emb[74] | 从交互样本中无监督地学习对手表征 | 提取同时具有策略提升效果和对手区分度的表征信息 | 无需领域知识,通用性强,适用大多数DRL算法 | 无法独立推断,用于辅助其他DRL算法决策 |
| RFM[73] | 采用图网络学习智能体的社会关系表征 | 通过边缘属性、节点等图结构信息预测对手行动、评估对手社会关系强度 | 量化智能体交互的社会属性,网络结构具有较好拓展性 | 存在复杂交互关系的图网络计算困难 |
| 概率 推理 | P-BIT[76] | 多智能体DRL的最优策略形式化为推理私有信息的概率下界 | 使用信念模块根据友方行为推理其私有信息 | 提出不完美信息条件下通过行动与队友传递私有信息的方法 | 适用于简单的二人合作场景 |
| ROMMEO[78] | 多智能体DRL形式化为基于对手模型的最优策略变分推理 | 预测对手行动,用于实现学习最优策略的推理任务 | 提出最大熵目标的正则化的对手建模方法 | 在线优化参数,训练时间长.默认对手目标已知,无法适应未知智能体 |
| 自我- 他人交互 | SOM[79] | 基于自身策略推理对手可能的目标,用于支撑决策 | 建立拟合对手策略的神经网络,通过优化对手策略反向推断对手的目标 | 无需额外模型和参数显式建模,仿照自身模型推理任意数量规模对手 | 智能体与对手共享目标,并且奖励结构取决于目标 |
| LOLA[81] | 考虑具有学习能力的对手,解释对手学习参数的更新对自身策略影响 | 建模对手的价值函数,求其二阶导优化策略梯度 | 策略更新中增加了对手参数更新项,通过泰勒展开构造成高阶梯度项 | 默认对手使用可梯度优化的方法,并且无法察觉LOLA对其模型进行利用 |
4 应用场景DRL-OM方法起初应用于游戏领域的智能体建模,随着深度强化学习算法在现实场景中的落地应用,DRL-OM技术也拓展到军事仿真、公共安全等诸多领域. ...
Recurrent World Models Facilitate Policy Evolution
1
2018
... 学习表征的建模方法以无监督的学习形式从观测信息中提取对手的表征信息,用于增强深度学习网络的输入信息,无需数据集、奖励等先验知识,提取表征的常见结构包括图神经网络架构[73]、前馈神经网络[74]、循环神经网络[75]等. ...
Learning to Communicate Implicitly by Actions
2
2020
... Tian等[76]提出借助行动隐式通信的(policy-belief-iteration, P-BIT)多智能体团队合作方法,P-BIT方法用于团队合作中的队友建模,模型用于推理队友的私有信息,并将其作为条件最大化的条件概率下界来求解最优策略.该算法将使用期望极大(EM)算法求解决策推理问题.P-BIT在具体流程中建立信念模块,将观测动作作为输入,输出队友的私有信息,策略模块利用私有信息推测动作分布,2个模块迭代训练.为了实现协作场景下的多智能体隐式通信,该算法为策略模块的训练设置辅助奖励,以鼓励智能体信息交换. ...
... Summary of research motivation, innovation points and limitations of implicit based opponent modeling methods
Table 4| 类别 | 算法 | 研究动机 | 模型特点 | 创新点 | 局限性 |
|---|
| 辅助 任务 | DRON[26] | 设计挖掘不同对手策略隐藏特征的神经网络 | 使用MLP处理对手行动,将表征信息用于强化学习任务 | 提取对手特征用于DRL算法决策 | 手工提取输入专家网络的特征,可采用RNN改进 |
| DIPQN[71] | 从观测直接提取对手策略特征,训练对手建模的辅助任务 | 策略特征网络学习从观测提取表征,并通过行为克隆的准确性修正网络 | 设计了调节最大奖励与对手建模的自适应损失函数 | 采用经验回放池离线训练,学习的对手策略具有较大样本方差 |
| AMS-A3C[72] | 在强化学习过程中,制订估计其他智能体策略的辅助任务 | 决策网络与模仿决策的对手模型共享结构、参数,降低模型学习成本 | 提出参数共享、策略表征2套方案,将对手建模融合进A3C算法 | 对手模型参数敏感,难以应对复杂场景、具有学习能力的对手 |
| 学习 表征 | PPO-Emb[74] | 从交互样本中无监督地学习对手表征 | 提取同时具有策略提升效果和对手区分度的表征信息 | 无需领域知识,通用性强,适用大多数DRL算法 | 无法独立推断,用于辅助其他DRL算法决策 |
| RFM[73] | 采用图网络学习智能体的社会关系表征 | 通过边缘属性、节点等图结构信息预测对手行动、评估对手社会关系强度 | 量化智能体交互的社会属性,网络结构具有较好拓展性 | 存在复杂交互关系的图网络计算困难 |
| 概率 推理 | P-BIT[76] | 多智能体DRL的最优策略形式化为推理私有信息的概率下界 | 使用信念模块根据友方行为推理其私有信息 | 提出不完美信息条件下通过行动与队友传递私有信息的方法 | 适用于简单的二人合作场景 |
| ROMMEO[78] | 多智能体DRL形式化为基于对手模型的最优策略变分推理 | 预测对手行动,用于实现学习最优策略的推理任务 | 提出最大熵目标的正则化的对手建模方法 | 在线优化参数,训练时间长.默认对手目标已知,无法适应未知智能体 |
| 自我- 他人交互 | SOM[79] | 基于自身策略推理对手可能的目标,用于支撑决策 | 建立拟合对手策略的神经网络,通过优化对手策略反向推断对手的目标 | 无需额外模型和参数显式建模,仿照自身模型推理任意数量规模对手 | 智能体与对手共享目标,并且奖励结构取决于目标 |
| LOLA[81] | 考虑具有学习能力的对手,解释对手学习参数的更新对自身策略影响 | 建模对手的价值函数,求其二阶导优化策略梯度 | 策略更新中增加了对手参数更新项,通过泰勒展开构造成高阶梯度项 | 默认对手使用可梯度优化的方法,并且无法察觉LOLA对其模型进行利用 |
4 应用场景DRL-OM方法起初应用于游戏领域的智能体建模,随着深度强化学习算法在现实场景中的落地应用,DRL-OM技术也拓展到军事仿真、公共安全等诸多领域. ...
Soft Actor-critic Algorithms and Applications
1
1812
... 最大熵学习[77]常用在单智能体的策略探索中,用于保证学习策略的多样性.Zheng等[78]将多智能体RL问题建模成贝叶斯推理并提出基于最大熵目标的正则化对手模型算法(regularized opponent model with maximum entropy objective, ROMMEO).ROMMEO将智能体所获得的回报看作学习最优策略的概率下界,而优化智能体的回报需要对手行动.因此,为了最大化智能体回报,ROMMEO将对手建模策略和对手动作分布之间的KL散度作为惩罚项预测对手行动,从而保持当前对手模型的真实性.同时,以增加智能体策略熵的方式提升策略随机性,用于寻找自身的最优策略. ...
A Regularized Opponent Model with Maximum Entropy Objective
3
1905
... 最大熵学习[77]常用在单智能体的策略探索中,用于保证学习策略的多样性.Zheng等[78]将多智能体RL问题建模成贝叶斯推理并提出基于最大熵目标的正则化对手模型算法(regularized opponent model with maximum entropy objective, ROMMEO).ROMMEO将智能体所获得的回报看作学习最优策略的概率下界,而优化智能体的回报需要对手行动.因此,为了最大化智能体回报,ROMMEO将对手建模策略和对手动作分布之间的KL散度作为惩罚项预测对手行动,从而保持当前对手模型的真实性.同时,以增加智能体策略熵的方式提升策略随机性,用于寻找自身的最优策略. ...
... Summary of research motivation, innovation points and limitations of implicit based opponent modeling methods
Table 4| 类别 | 算法 | 研究动机 | 模型特点 | 创新点 | 局限性 |
|---|
| 辅助 任务 | DRON[26] | 设计挖掘不同对手策略隐藏特征的神经网络 | 使用MLP处理对手行动,将表征信息用于强化学习任务 | 提取对手特征用于DRL算法决策 | 手工提取输入专家网络的特征,可采用RNN改进 |
| DIPQN[71] | 从观测直接提取对手策略特征,训练对手建模的辅助任务 | 策略特征网络学习从观测提取表征,并通过行为克隆的准确性修正网络 | 设计了调节最大奖励与对手建模的自适应损失函数 | 采用经验回放池离线训练,学习的对手策略具有较大样本方差 |
| AMS-A3C[72] | 在强化学习过程中,制订估计其他智能体策略的辅助任务 | 决策网络与模仿决策的对手模型共享结构、参数,降低模型学习成本 | 提出参数共享、策略表征2套方案,将对手建模融合进A3C算法 | 对手模型参数敏感,难以应对复杂场景、具有学习能力的对手 |
| 学习 表征 | PPO-Emb[74] | 从交互样本中无监督地学习对手表征 | 提取同时具有策略提升效果和对手区分度的表征信息 | 无需领域知识,通用性强,适用大多数DRL算法 | 无法独立推断,用于辅助其他DRL算法决策 |
| RFM[73] | 采用图网络学习智能体的社会关系表征 | 通过边缘属性、节点等图结构信息预测对手行动、评估对手社会关系强度 | 量化智能体交互的社会属性,网络结构具有较好拓展性 | 存在复杂交互关系的图网络计算困难 |
| 概率 推理 | P-BIT[76] | 多智能体DRL的最优策略形式化为推理私有信息的概率下界 | 使用信念模块根据友方行为推理其私有信息 | 提出不完美信息条件下通过行动与队友传递私有信息的方法 | 适用于简单的二人合作场景 |
| ROMMEO[78] | 多智能体DRL形式化为基于对手模型的最优策略变分推理 | 预测对手行动,用于实现学习最优策略的推理任务 | 提出最大熵目标的正则化的对手建模方法 | 在线优化参数,训练时间长.默认对手目标已知,无法适应未知智能体 |
| 自我- 他人交互 | SOM[79] | 基于自身策略推理对手可能的目标,用于支撑决策 | 建立拟合对手策略的神经网络,通过优化对手策略反向推断对手的目标 | 无需额外模型和参数显式建模,仿照自身模型推理任意数量规模对手 | 智能体与对手共享目标,并且奖励结构取决于目标 |
| LOLA[81] | 考虑具有学习能力的对手,解释对手学习参数的更新对自身策略影响 | 建模对手的价值函数,求其二阶导优化策略梯度 | 策略更新中增加了对手参数更新项,通过泰勒展开构造成高阶梯度项 | 默认对手使用可梯度优化的方法,并且无法察觉LOLA对其模型进行利用 |
4 应用场景DRL-OM方法起初应用于游戏领域的智能体建模,随着深度强化学习算法在现实场景中的落地应用,DRL-OM技术也拓展到军事仿真、公共安全等诸多领域. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Modeling Others Using Oneself in Multi-agent Reinforcement Learning
2
2018
... 前文所述方法大多通过推理对手真实行动,观察得出对手模型的特征.与此不同的是,许多研究考虑从衡量智能体自身受到对手交互影响的角度建立对手模型.例如,当所有智能体具有相同的输入变量和模型结构,以及近似的任务目标时,智能体与对手行动的差别取决于目标奖励.根据这个理念,Raileanu等[79]提出了一种推断未知对手目标的建模方法,即自我-他人建模(self-other modeling, SOM).与以往的方法不同,SOM不是预测对手策略作为手段,而是估计对手的目标.SOM智能体使用了2个决策网络,第1个用于计算智能体自身策略,第2个是学习对手策略的对手模型.并且SOM显式地建立了智能体的目标这一概念,将目标作为对手模型的参数,根据对手模型输出与观测真实对手行动反向传播调节参数得到对手目标.SOM能够在合作和竞争性的环境中推断目标,预测出对手的行为,表现优于独立决策智能体和基于DRQN智能体.SOM算法的优点是智能体以自身模型推断对手,不需要设定额外参数来建立对手模型,便于推断任意数量智能体的目标.其缺点是具有较强的假设,即假定智能体共享一组目标,每个个体在事件开始时都被分配一个目标,并且奖励结构取决于他们所分配的共同目标.此外,SOM算法每步都需要在线优化目标估计网络,决策时间长. ...
... Summary of research motivation, innovation points and limitations of implicit based opponent modeling methods
Table 4| 类别 | 算法 | 研究动机 | 模型特点 | 创新点 | 局限性 |
|---|
| 辅助 任务 | DRON[26] | 设计挖掘不同对手策略隐藏特征的神经网络 | 使用MLP处理对手行动,将表征信息用于强化学习任务 | 提取对手特征用于DRL算法决策 | 手工提取输入专家网络的特征,可采用RNN改进 |
| DIPQN[71] | 从观测直接提取对手策略特征,训练对手建模的辅助任务 | 策略特征网络学习从观测提取表征,并通过行为克隆的准确性修正网络 | 设计了调节最大奖励与对手建模的自适应损失函数 | 采用经验回放池离线训练,学习的对手策略具有较大样本方差 |
| AMS-A3C[72] | 在强化学习过程中,制订估计其他智能体策略的辅助任务 | 决策网络与模仿决策的对手模型共享结构、参数,降低模型学习成本 | 提出参数共享、策略表征2套方案,将对手建模融合进A3C算法 | 对手模型参数敏感,难以应对复杂场景、具有学习能力的对手 |
| 学习 表征 | PPO-Emb[74] | 从交互样本中无监督地学习对手表征 | 提取同时具有策略提升效果和对手区分度的表征信息 | 无需领域知识,通用性强,适用大多数DRL算法 | 无法独立推断,用于辅助其他DRL算法决策 |
| RFM[73] | 采用图网络学习智能体的社会关系表征 | 通过边缘属性、节点等图结构信息预测对手行动、评估对手社会关系强度 | 量化智能体交互的社会属性,网络结构具有较好拓展性 | 存在复杂交互关系的图网络计算困难 |
| 概率 推理 | P-BIT[76] | 多智能体DRL的最优策略形式化为推理私有信息的概率下界 | 使用信念模块根据友方行为推理其私有信息 | 提出不完美信息条件下通过行动与队友传递私有信息的方法 | 适用于简单的二人合作场景 |
| ROMMEO[78] | 多智能体DRL形式化为基于对手模型的最优策略变分推理 | 预测对手行动,用于实现学习最优策略的推理任务 | 提出最大熵目标的正则化的对手建模方法 | 在线优化参数,训练时间长.默认对手目标已知,无法适应未知智能体 |
| 自我- 他人交互 | SOM[79] | 基于自身策略推理对手可能的目标,用于支撑决策 | 建立拟合对手策略的神经网络,通过优化对手策略反向推断对手的目标 | 无需额外模型和参数显式建模,仿照自身模型推理任意数量规模对手 | 智能体与对手共享目标,并且奖励结构取决于目标 |
| LOLA[81] | 考虑具有学习能力的对手,解释对手学习参数的更新对自身策略影响 | 建模对手的价值函数,求其二阶导优化策略梯度 | 策略更新中增加了对手参数更新项,通过泰勒展开构造成高阶梯度项 | 默认对手使用可梯度优化的方法,并且无法察觉LOLA对其模型进行利用 |
4 应用场景DRL-OM方法起初应用于游戏领域的智能体建模,随着深度强化学习算法在现实场景中的落地应用,DRL-OM技术也拓展到军事仿真、公共安全等诸多领域. ...
Multi-agent Learning with Policy Prediction
3
2010
... 智能体需要考虑交互过程中的对手学习过程,而非将其看作静态环境的一部分.根据这一思想,Zhang等[80-81]提出需要在更新自身策略梯度时考虑对手学习策略的梯度更新,并将对手的学习过程考虑在自身策略优化中.假设智能体和对手的模型参数分别为和,与优化的常规梯度优化方法不同,研究者认为具有对手学习过程的能够避免学习静态的对手策略.Zhang等[80]假定对是不可微的情况下,在二人博弈实验中取得均衡.Foerster等[81]提出的LOLA(learning with opponent learning awareness)算法则在对可微的假设上利用对手学习过程优化策略,提出借助对手价值函数的二阶优化项优化自身梯度.LOLA算法在囚徒博弈中实现最大双方价值的合作策略,它的缺点是无法在对手策略不可微时使用,并且忽略了对手能够察觉到LOLA对其建模并反制的情形. ...
... [80]假定对是不可微的情况下,在二人博弈实验中取得均衡.Foerster等[81]提出的LOLA(learning with opponent learning awareness)算法则在对可微的假设上利用对手学习过程优化策略,提出借助对手价值函数的二阶优化项优化自身梯度.LOLA算法在囚徒博弈中实现最大双方价值的合作策略,它的缺点是无法在对手策略不可微时使用,并且忽略了对手能够察觉到LOLA对其建模并反制的情形. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Learning with Opponent-learning Awareness
3
2018
... 智能体需要考虑交互过程中的对手学习过程,而非将其看作静态环境的一部分.根据这一思想,Zhang等[80-81]提出需要在更新自身策略梯度时考虑对手学习策略的梯度更新,并将对手的学习过程考虑在自身策略优化中.假设智能体和对手的模型参数分别为和,与优化的常规梯度优化方法不同,研究者认为具有对手学习过程的能够避免学习静态的对手策略.Zhang等[80]假定对是不可微的情况下,在二人博弈实验中取得均衡.Foerster等[81]提出的LOLA(learning with opponent learning awareness)算法则在对可微的假设上利用对手学习过程优化策略,提出借助对手价值函数的二阶优化项优化自身梯度.LOLA算法在囚徒博弈中实现最大双方价值的合作策略,它的缺点是无法在对手策略不可微时使用,并且忽略了对手能够察觉到LOLA对其建模并反制的情形. ...
... [81]提出的LOLA(learning with opponent learning awareness)算法则在对可微的假设上利用对手学习过程优化策略,提出借助对手价值函数的二阶优化项优化自身梯度.LOLA算法在囚徒博弈中实现最大双方价值的合作策略,它的缺点是无法在对手策略不可微时使用,并且忽略了对手能够察觉到LOLA对其建模并反制的情形. ...
... Summary of research motivation, innovation points and limitations of implicit based opponent modeling methods
Table 4| 类别 | 算法 | 研究动机 | 模型特点 | 创新点 | 局限性 |
|---|
| 辅助 任务 | DRON[26] | 设计挖掘不同对手策略隐藏特征的神经网络 | 使用MLP处理对手行动,将表征信息用于强化学习任务 | 提取对手特征用于DRL算法决策 | 手工提取输入专家网络的特征,可采用RNN改进 |
| DIPQN[71] | 从观测直接提取对手策略特征,训练对手建模的辅助任务 | 策略特征网络学习从观测提取表征,并通过行为克隆的准确性修正网络 | 设计了调节最大奖励与对手建模的自适应损失函数 | 采用经验回放池离线训练,学习的对手策略具有较大样本方差 |
| AMS-A3C[72] | 在强化学习过程中,制订估计其他智能体策略的辅助任务 | 决策网络与模仿决策的对手模型共享结构、参数,降低模型学习成本 | 提出参数共享、策略表征2套方案,将对手建模融合进A3C算法 | 对手模型参数敏感,难以应对复杂场景、具有学习能力的对手 |
| 学习 表征 | PPO-Emb[74] | 从交互样本中无监督地学习对手表征 | 提取同时具有策略提升效果和对手区分度的表征信息 | 无需领域知识,通用性强,适用大多数DRL算法 | 无法独立推断,用于辅助其他DRL算法决策 |
| RFM[73] | 采用图网络学习智能体的社会关系表征 | 通过边缘属性、节点等图结构信息预测对手行动、评估对手社会关系强度 | 量化智能体交互的社会属性,网络结构具有较好拓展性 | 存在复杂交互关系的图网络计算困难 |
| 概率 推理 | P-BIT[76] | 多智能体DRL的最优策略形式化为推理私有信息的概率下界 | 使用信念模块根据友方行为推理其私有信息 | 提出不完美信息条件下通过行动与队友传递私有信息的方法 | 适用于简单的二人合作场景 |
| ROMMEO[78] | 多智能体DRL形式化为基于对手模型的最优策略变分推理 | 预测对手行动,用于实现学习最优策略的推理任务 | 提出最大熵目标的正则化的对手建模方法 | 在线优化参数,训练时间长.默认对手目标已知,无法适应未知智能体 |
| 自我- 他人交互 | SOM[79] | 基于自身策略推理对手可能的目标,用于支撑决策 | 建立拟合对手策略的神经网络,通过优化对手策略反向推断对手的目标 | 无需额外模型和参数显式建模,仿照自身模型推理任意数量规模对手 | 智能体与对手共享目标,并且奖励结构取决于目标 |
| LOLA[81] | 考虑具有学习能力的对手,解释对手学习参数的更新对自身策略影响 | 建模对手的价值函数,求其二阶导优化策略梯度 | 策略更新中增加了对手参数更新项,通过泰勒展开构造成高阶梯度项 | 默认对手使用可梯度优化的方法,并且无法察觉LOLA对其模型进行利用 |
4 应用场景DRL-OM方法起初应用于游戏领域的智能体建模,随着深度强化学习算法在现实场景中的落地应用,DRL-OM技术也拓展到军事仿真、公共安全等诸多领域. ...
DeepStack: Expert-Level Artificial Intelligence in No-Limit Poker
1
2017
... 棋牌类游戏具有不完美信息序贯决策的特性,因此这类游戏的智能体广泛采用基于反事实遗憾值最小化的显式建模方法.2017年1月加拿大阿尔伯特大学开发的DeepStack[82]在无限制德州扑克单挑赛中战胜所有参与的人类玩家.DeepStack采用了基于CFR理论的递归推理方法,通过强化学习值函数用于截断博弈子树,以对手遗憾值和自身范围解算残局.同年,卡耐基梅隆大学Brown等[83]研发出的Libratus在无限制德州扑克单挑赛中击败了更强的人类职业选手.Libratus在游戏初始将博弈抽象表示为“蓝图”,以便基于蒙特卡罗CFR算法的求解.游戏过程的中后期,构建“蓝图”策略内计算的嵌套子博弈求解残局,并且针对可被对手利用的弱点提出自我改进. ...
Superhuman AI for Heads-up No-limit Poker: Libratus Beats Top Professionals
1
2017
... 棋牌类游戏具有不完美信息序贯决策的特性,因此这类游戏的智能体广泛采用基于反事实遗憾值最小化的显式建模方法.2017年1月加拿大阿尔伯特大学开发的DeepStack[82]在无限制德州扑克单挑赛中战胜所有参与的人类玩家.DeepStack采用了基于CFR理论的递归推理方法,通过强化学习值函数用于截断博弈子树,以对手遗憾值和自身范围解算残局.同年,卡耐基梅隆大学Brown等[83]研发出的Libratus在无限制德州扑克单挑赛中击败了更强的人类职业选手.Libratus在游戏初始将博弈抽象表示为“蓝图”,以便基于蒙特卡罗CFR算法的求解.游戏过程的中后期,构建“蓝图”策略内计算的嵌套子博弈求解残局,并且针对可被对手利用的弱点提出自我改进. ...
Enhanced Rolling Horizon Evolution Algorithm with Opponent Model Learning
3
... 对于街机格斗类游戏,2020年Tang等[84]提出自适应对手模型的滚动时域进化算法,采用交叉熵、Q学习和策略梯度等多种监督学习和强化学习等辅助任务的隐式建模方法优化预测对手行动的有效性.最终基于该算法的智能体击败了基于MCTS模型的智能体,在IEEE CoG举办的格斗游戏AI竞赛上取得最终冠军.此外,对手建模也广泛应用于第一人称射击[85-86]、足球机器人[87-89]等游戏的人工智能. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
... 现实应用中的即时决策场景十分常见,如竞技体育、战术决策等需要在短时间内做出反应决策.在强实时性的场景中,智能体面临着同时考虑计算准确性和效率的问题.Tang等[84]在滚动时域算法的基础上,使用深度强化学习预测对手行动,优化对手建模的有效性,实现了双人格斗游戏的博弈推理.然而,在多人在线游戏、大规模作战仿真等应用[10]中,面临的是多人实时博弈这种更为复杂的情况,实现这类场景下对手建模的实时性决策是亟需解决的难题. ...
Combo-action: Training Agent for FPS Game with Auxiliary Tasks
1
2019
... 对于街机格斗类游戏,2020年Tang等[84]提出自适应对手模型的滚动时域进化算法,采用交叉熵、Q学习和策略梯度等多种监督学习和强化学习等辅助任务的隐式建模方法优化预测对手行动的有效性.最终基于该算法的智能体击败了基于MCTS模型的智能体,在IEEE CoG举办的格斗游戏AI竞赛上取得最终冠军.此外,对手建模也广泛应用于第一人称射击[85-86]、足球机器人[87-89]等游戏的人工智能. ...
Determinants of We-intention for Continue Playing FPS Game: Cooperation and Competition
1
2020
... 对于街机格斗类游戏,2020年Tang等[84]提出自适应对手模型的滚动时域进化算法,采用交叉熵、Q学习和策略梯度等多种监督学习和强化学习等辅助任务的隐式建模方法优化预测对手行动的有效性.最终基于该算法的智能体击败了基于MCTS模型的智能体,在IEEE CoG举办的格斗游戏AI竞赛上取得最终冠军.此外,对手建模也广泛应用于第一人称射击[85-86]、足球机器人[87-89]等游戏的人工智能. ...
Model-based Opponent Modeling
3
2108
... 对于街机格斗类游戏,2020年Tang等[84]提出自适应对手模型的滚动时域进化算法,采用交叉熵、Q学习和策略梯度等多种监督学习和强化学习等辅助任务的隐式建模方法优化预测对手行动的有效性.最终基于该算法的智能体击败了基于MCTS模型的智能体,在IEEE CoG举办的格斗游戏AI竞赛上取得最终冠军.此外,对手建模也广泛应用于第一人称射击[85-86]、足球机器人[87-89]等游戏的人工智能. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
... 为此,Yu等[87]提出一种基于环境模型的贝叶斯递归推理方法,通过贝叶斯定理分配对手采取每种策略的权重,并将不同递归层次的策略组合构成对手策略,该算法在保证效率的同时避免了获取对手先验知识.Zhang等[132]将有模型强化学习的模型误差分为环境动态误差和对手模型误差,开发了自适应调整采样长度的对手建模误差控制方法,使用虚拟的对手和环境模型自演交互以扩充样本数据,达到高效利用数据的目的. ...
Opponent Modeling in RoboCup Soccer Simulation
0
2018
L2e: Learning to Exploit Your Opponent
1
2102
... 对于街机格斗类游戏,2020年Tang等[84]提出自适应对手模型的滚动时域进化算法,采用交叉熵、Q学习和策略梯度等多种监督学习和强化学习等辅助任务的隐式建模方法优化预测对手行动的有效性.最终基于该算法的智能体击败了基于MCTS模型的智能体,在IEEE CoG举办的格斗游戏AI竞赛上取得最终冠军.此外,对手建模也广泛应用于第一人称射击[85-86]、足球机器人[87-89]等游戏的人工智能. ...
Employing Game Theory and Computational Intelligence to Find the Optimal Strategy of an Autonomous Underwater Vehicle Against A Submarine
2
2016
... DRL-OM技术在军事仿真领域里具有广阔的发展前景.作为作战中辅助决策的手段,DRL-OM能够从战场获取的粗糙感知信息中精炼态势、意图,以增强判别意图遮蔽或战术欺骗的能力,从而能够为战场指挥控制节点提供高层决策支撑.广泛应用于水下航行器作战[90]、无人机集群对抗[91-93]、模拟蓝军对抗演习[94-96]等军事作战场景. ...
... 2016年,Dzieńkowski等[90]研究了考虑对手潜艇探测的自动水下机器人最优行动策略,提出一种应用于复杂海况的改进MiniMax均衡策略显式DRL-OM方法,利用神经网络模型灵活评估效用函数,并且由遗传算法调整模型参数. ...
Autonomous Air Combat Maneuver Decision Using Bayesian Inference and Moving Horizon Optimization
2
2018
... DRL-OM技术在军事仿真领域里具有广阔的发展前景.作为作战中辅助决策的手段,DRL-OM能够从战场获取的粗糙感知信息中精炼态势、意图,以增强判别意图遮蔽或战术欺骗的能力,从而能够为战场指挥控制节点提供高层决策支撑.广泛应用于水下航行器作战[90]、无人机集群对抗[91-93]、模拟蓝军对抗演习[94-96]等军事作战场景. ...
... 2018年,空军工程大学的Huang等[91]在空战格斗中建立自主决策无人机飞行系统,利用贝叶斯推理和滚动时域优化(Bayesian inference and moving horizon optimization, BI&MHO)判断空战态势,并且基于机动惯性原理建立了对手飞行器的空中位置预测.2020年,空军工程大学的Zhou等[92]提出模拟人脑学习机制的智能空战学习框架,根据认知科学中对学习、知识和记忆的研究构建了大脑的认知机制模型.基于此模型和人类的推理能力,该方法建立了一个长期短期记忆的层次化多线程学习系统.该方法属于基于心智理论递归推理的隐式DRL-OM方法,相较BI&MHO具有更强的态势感知和对手动作预测能力. ...
Learning System for Air Combat Decision Inspired by Cognitive Mechanisms of the Brain
1
2020
... 2018年,空军工程大学的Huang等[91]在空战格斗中建立自主决策无人机飞行系统,利用贝叶斯推理和滚动时域优化(Bayesian inference and moving horizon optimization, BI&MHO)判断空战态势,并且基于机动惯性原理建立了对手飞行器的空中位置预测.2020年,空军工程大学的Zhou等[92]提出模拟人脑学习机制的智能空战学习框架,根据认知科学中对学习、知识和记忆的研究构建了大脑的认知机制模型.基于此模型和人类的推理能力,该方法建立了一个长期短期记忆的层次化多线程学习系统.该方法属于基于心智理论递归推理的隐式DRL-OM方法,相较BI&MHO具有更强的态势感知和对手动作预测能力. ...
基于深度强化学习的多机协同空战方法研究
1
2021
... DRL-OM技术在军事仿真领域里具有广阔的发展前景.作为作战中辅助决策的手段,DRL-OM能够从战场获取的粗糙感知信息中精炼态势、意图,以增强判别意图遮蔽或战术欺骗的能力,从而能够为战场指挥控制节点提供高层决策支撑.广泛应用于水下航行器作战[90]、无人机集群对抗[91-93]、模拟蓝军对抗演习[94-96]等军事作战场景. ...
Research on Multi-aircraft Cooperative Air Combat Method Based on Deep Reinforcement Learning
1
2021
... DRL-OM技术在军事仿真领域里具有广阔的发展前景.作为作战中辅助决策的手段,DRL-OM能够从战场获取的粗糙感知信息中精炼态势、意图,以增强判别意图遮蔽或战术欺骗的能力,从而能够为战场指挥控制节点提供高层决策支撑.广泛应用于水下航行器作战[90]、无人机集群对抗[91-93]、模拟蓝军对抗演习[94-96]等军事作战场景. ...
Constructive Machine-learning Battles with Adversary-Tactics
2
... DRL-OM技术在军事仿真领域里具有广阔的发展前景.作为作战中辅助决策的手段,DRL-OM能够从战场获取的粗糙感知信息中精炼态势、意图,以增强判别意图遮蔽或战术欺骗的能力,从而能够为战场指挥控制节点提供高层决策支撑.广泛应用于水下航行器作战[90]、无人机集群对抗[91-93]、模拟蓝军对抗演习[94-96]等军事作战场景. ...
... 2020年美国国防高级研究计划局(DARPA)提出“针对敌方战术的建设性机器学习作战”(constructive machine-learning battles with adversary tactics, COMBAT)项目[94],旨在建立多组由机器学习生成战术的模拟蓝军分队,通过仿真作战环境充分挖掘士兵现有战术行为的缺陷并学习制定对策.同时,该项目结合深度强化学习算法和博弈论实现复杂战场环境决策,并利用OneSAF系统[95]评估人工智能系统在人机协同回路中的战术有效性.2021年,中科院的Liu等[96]将对手建模运用在兵棋推演中.该方法在静态地图添加注意力机制,赋予其动态特征,利用CNN网络提取战场态势表征,并使用位置预测模型根据长短时记忆网络预测兵力的行动轨迹,是一种典型的基于表征学习的隐式DRL-OM方法. ...
OneSAF: a next Generation Simulation Modeling the Contemporary Operating Environment
1
2005
... 2020年美国国防高级研究计划局(DARPA)提出“针对敌方战术的建设性机器学习作战”(constructive machine-learning battles with adversary tactics, COMBAT)项目[94],旨在建立多组由机器学习生成战术的模拟蓝军分队,通过仿真作战环境充分挖掘士兵现有战术行为的缺陷并学习制定对策.同时,该项目结合深度强化学习算法和博弈论实现复杂战场环境决策,并利用OneSAF系统[95]评估人工智能系统在人机协同回路中的战术有效性.2021年,中科院的Liu等[96]将对手建模运用在兵棋推演中.该方法在静态地图添加注意力机制,赋予其动态特征,利用CNN网络提取战场态势表征,并使用位置预测模型根据长短时记忆网络预测兵力的行动轨迹,是一种典型的基于表征学习的隐式DRL-OM方法. ...
Tactical Intention Recognition in Wargame
2
2021
... DRL-OM技术在军事仿真领域里具有广阔的发展前景.作为作战中辅助决策的手段,DRL-OM能够从战场获取的粗糙感知信息中精炼态势、意图,以增强判别意图遮蔽或战术欺骗的能力,从而能够为战场指挥控制节点提供高层决策支撑.广泛应用于水下航行器作战[90]、无人机集群对抗[91-93]、模拟蓝军对抗演习[94-96]等军事作战场景. ...
... 2020年美国国防高级研究计划局(DARPA)提出“针对敌方战术的建设性机器学习作战”(constructive machine-learning battles with adversary tactics, COMBAT)项目[94],旨在建立多组由机器学习生成战术的模拟蓝军分队,通过仿真作战环境充分挖掘士兵现有战术行为的缺陷并学习制定对策.同时,该项目结合深度强化学习算法和博弈论实现复杂战场环境决策,并利用OneSAF系统[95]评估人工智能系统在人机协同回路中的战术有效性.2021年,中科院的Liu等[96]将对手建模运用在兵棋推演中.该方法在静态地图添加注意力机制,赋予其动态特征,利用CNN网络提取战场态势表征,并使用位置预测模型根据长短时记忆网络预测兵力的行动轨迹,是一种典型的基于表征学习的隐式DRL-OM方法. ...
安全博弈论研究综述
1
2015
... 在公共安全领域,DRL-OM的研究主要集中在博弈模型求解.公共安全可以看作是一类安防博弈问题,相较一般决策问题,安防博弈需要考虑智能化适应对手行为所带来的影响,表现出极强的对抗性和动态性.安防博弈问题与对手建模研究一脉相承[97],其核心是通过博弈建模攻防双方的交互过程.根据公共安全的研究问题,对手建模的应用背景可以是交通网络安全[98-99],区域防恐威胁[100-101]、自动驾驶[102-103]、信息网络安全[104]等场景. ...
An Overview of Security Games
1
2015
... 在公共安全领域,DRL-OM的研究主要集中在博弈模型求解.公共安全可以看作是一类安防博弈问题,相较一般决策问题,安防博弈需要考虑智能化适应对手行为所带来的影响,表现出极强的对抗性和动态性.安防博弈问题与对手建模研究一脉相承[97],其核心是通过博弈建模攻防双方的交互过程.根据公共安全的研究问题,对手建模的应用背景可以是交通网络安全[98-99],区域防恐威胁[100-101]、自动驾驶[102-103]、信息网络安全[104]等场景. ...
Optimal Escape Interdiction on Transportation Networks
2
2017
... 在公共安全领域,DRL-OM的研究主要集中在博弈模型求解.公共安全可以看作是一类安防博弈问题,相较一般决策问题,安防博弈需要考虑智能化适应对手行为所带来的影响,表现出极强的对抗性和动态性.安防博弈问题与对手建模研究一脉相承[97],其核心是通过博弈建模攻防双方的交互过程.根据公共安全的研究问题,对手建模的应用背景可以是交通网络安全[98-99],区域防恐威胁[100-101]、自动驾驶[102-103]、信息网络安全[104]等场景. ...
... 针对交通网络问题,Zhang等[98]提出了在道路网络中封锁犯罪分子逃逸路线的研究,设计一种封锁道路的攻击者-防御者安全博弈模型,并结合基于混合整数线性规划公式的最佳响应和基于高效双Oracle算法[58]的有效近似来计算最佳的防御策略.Xue等[99]将NFSP模型运用在大规模扩展式的网络安防博弈(network security games, NSGs)中,并使用斯坦伯格博弈的形式求解.首先,模型将NFSP中的最佳响应策略网络从行动-状态改造为行动-价值的映射,使NSGs中最佳响应的计算成为可能.随后,将NFSP智能体的平均策略网络转换为基于度量的分类器,为智能体提供高水平的行动,通过学习高效的图节点嵌入来利用NSGs图中包含的信息,模型在可扩展性和质量方面都有显著提升. ...
Solving Large-scale Extensive-form Network Security Games via Neural Fictitious Self-play
2
2106
... 在公共安全领域,DRL-OM的研究主要集中在博弈模型求解.公共安全可以看作是一类安防博弈问题,相较一般决策问题,安防博弈需要考虑智能化适应对手行为所带来的影响,表现出极强的对抗性和动态性.安防博弈问题与对手建模研究一脉相承[97],其核心是通过博弈建模攻防双方的交互过程.根据公共安全的研究问题,对手建模的应用背景可以是交通网络安全[98-99],区域防恐威胁[100-101]、自动驾驶[102-103]、信息网络安全[104]等场景. ...
... 针对交通网络问题,Zhang等[98]提出了在道路网络中封锁犯罪分子逃逸路线的研究,设计一种封锁道路的攻击者-防御者安全博弈模型,并结合基于混合整数线性规划公式的最佳响应和基于高效双Oracle算法[58]的有效近似来计算最佳的防御策略.Xue等[99]将NFSP模型运用在大规模扩展式的网络安防博弈(network security games, NSGs)中,并使用斯坦伯格博弈的形式求解.首先,模型将NFSP中的最佳响应策略网络从行动-状态改造为行动-价值的映射,使NSGs中最佳响应的计算成为可能.随后,将NFSP智能体的平均策略网络转换为基于度量的分类器,为智能体提供高水平的行动,通过学习高效的图节点嵌入来利用NSGs图中包含的信息,模型在可扩展性和质量方面都有显著提升. ...
A Double Oracle Algorithm for Zero-sum Security Games on Graphs
2
2011
... 在公共安全领域,DRL-OM的研究主要集中在博弈模型求解.公共安全可以看作是一类安防博弈问题,相较一般决策问题,安防博弈需要考虑智能化适应对手行为所带来的影响,表现出极强的对抗性和动态性.安防博弈问题与对手建模研究一脉相承[97],其核心是通过博弈建模攻防双方的交互过程.根据公共安全的研究问题,对手建模的应用背景可以是交通网络安全[98-99],区域防恐威胁[100-101]、自动驾驶[102-103]、信息网络安全[104]等场景. ...
... 在区域防恐的应用中,Jain等[100]针对区域恐怖袭击研究城市警力资源分配,将问题建模成零和博弈,并使用双Oracle算法求解.现有研究缺乏动态调整资源分配的能力,因此,Zhang等[101]建立了一个模拟逃逸对手和有多个资源和实时信息的防御者之间交互过程的博弈模型,并设计增量策略生成算法求解. ...
Optimal Interdiction of Urban Criminals with the Aid of Real-time Information
2
2019
... 在公共安全领域,DRL-OM的研究主要集中在博弈模型求解.公共安全可以看作是一类安防博弈问题,相较一般决策问题,安防博弈需要考虑智能化适应对手行为所带来的影响,表现出极强的对抗性和动态性.安防博弈问题与对手建模研究一脉相承[97],其核心是通过博弈建模攻防双方的交互过程.根据公共安全的研究问题,对手建模的应用背景可以是交通网络安全[98-99],区域防恐威胁[100-101]、自动驾驶[102-103]、信息网络安全[104]等场景. ...
... 在区域防恐的应用中,Jain等[100]针对区域恐怖袭击研究城市警力资源分配,将问题建模成零和博弈,并使用双Oracle算法求解.现有研究缺乏动态调整资源分配的能力,因此,Zhang等[101]建立了一个模拟逃逸对手和有多个资源和实时信息的防御者之间交互过程的博弈模型,并设计增量策略生成算法求解. ...
Adaptive Game-theoretic Decision Making for Autonomous Vehicle Control at Roundabouts
2
2018
... 在公共安全领域,DRL-OM的研究主要集中在博弈模型求解.公共安全可以看作是一类安防博弈问题,相较一般决策问题,安防博弈需要考虑智能化适应对手行为所带来的影响,表现出极强的对抗性和动态性.安防博弈问题与对手建模研究一脉相承[97],其核心是通过博弈建模攻防双方的交互过程.根据公共安全的研究问题,对手建模的应用背景可以是交通网络安全[98-99],区域防恐威胁[100-101]、自动驾驶[102-103]、信息网络安全[104]等场景. ...
... 此外,DRL-OM关注车辆自动驾驶的道路安全性问题.Tian等[102]研究了交叉路口交通场景,建立表示环形交叉口两车交汇的博弈论模型,提出了一种基于车辆交互模型并适应对手车辆驾驶员类型的环形交叉口自我决策算法.Notomista等[103]提出一种意识增强的纳什均衡搜寻方法解决车辆竞速的交互问题,采用避免碰撞的约束条件刻画与对手车辆的竞争关系,并且在对手模型存在不确定性下提出鲁棒性保护条件. ...
Enhancing Game-theoretic Autonomous Car Racing Using Control Barrier Functions
2
2020
... 在公共安全领域,DRL-OM的研究主要集中在博弈模型求解.公共安全可以看作是一类安防博弈问题,相较一般决策问题,安防博弈需要考虑智能化适应对手行为所带来的影响,表现出极强的对抗性和动态性.安防博弈问题与对手建模研究一脉相承[97],其核心是通过博弈建模攻防双方的交互过程.根据公共安全的研究问题,对手建模的应用背景可以是交通网络安全[98-99],区域防恐威胁[100-101]、自动驾驶[102-103]、信息网络安全[104]等场景. ...
... 此外,DRL-OM关注车辆自动驾驶的道路安全性问题.Tian等[102]研究了交叉路口交通场景,建立表示环形交叉口两车交汇的博弈论模型,提出了一种基于车辆交互模型并适应对手车辆驾驶员类型的环形交叉口自我决策算法.Notomista等[103]提出一种意识增强的纳什均衡搜寻方法解决车辆竞速的交互问题,采用避免碰撞的约束条件刻画与对手车辆的竞争关系,并且在对手模型存在不确定性下提出鲁棒性保护条件. ...
Solving Non-zero Sum Multiagent Network Flow Security Games with Attack Costs
1
2012
... 在公共安全领域,DRL-OM的研究主要集中在博弈模型求解.公共安全可以看作是一类安防博弈问题,相较一般决策问题,安防博弈需要考虑智能化适应对手行为所带来的影响,表现出极强的对抗性和动态性.安防博弈问题与对手建模研究一脉相承[97],其核心是通过博弈建模攻防双方的交互过程.根据公共安全的研究问题,对手建模的应用背景可以是交通网络安全[98-99],区域防恐威胁[100-101]、自动驾驶[102-103]、信息网络安全[104]等场景. ...
Openai Gym
1
1606
... 针对深度强化学习领域内的通用问题,已有一系列学界公认的测试基准环境,如OpenAI GYM[105]、MuJoCo[106]、Fight ICE[107]等.基于这些开源框架,最先进的深度强化学习算法得以实现和对比.对于对手建模问题,特别是针对DRL-OM算法研究还没有形成统一的公共测试基准. ...
Mujoco: A Physics Engine for Model-based Control
1
2012
... 针对深度强化学习领域内的通用问题,已有一系列学界公认的测试基准环境,如OpenAI GYM[105]、MuJoCo[106]、Fight ICE[107]等.基于这些开源框架,最先进的深度强化学习算法得以实现和对比.对于对手建模问题,特别是针对DRL-OM算法研究还没有形成统一的公共测试基准. ...
Fighting Game Artificial Intelligence Competition Platform
2
2013
... 针对深度强化学习领域内的通用问题,已有一系列学界公认的测试基准环境,如OpenAI GYM[105]、MuJoCo[106]、Fight ICE[107]等.基于这些开源框架,最先进的深度强化学习算法得以实现和对比.对于对手建模问题,特别是针对DRL-OM算法研究还没有形成统一的公共测试基准. ...
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Markov Games as A Framework for Multi-agent Reinforcement Learning
1
1994
... 常见的实时环境仿真都是同步行动,即智能体间没有先后顺序,同时在环境中采取行动.此时若智能体能够完整观测状态,那么该博弈称为马尔科夫博弈(Markov game, MG)问题[108],实验场景例如囚徒困境问题和硬币博弈等.在MG问题中,如果各个智能体通过合作来最大化共同的回报,将其称为团队马尔科夫博弈[109](team Markov game, Team MG). ...
Reinforcement Learning to Play An Optimal Nash Equilibrium in Team Markov Games
1
2002
... 常见的实时环境仿真都是同步行动,即智能体间没有先后顺序,同时在环境中采取行动.此时若智能体能够完整观测状态,那么该博弈称为马尔科夫博弈(Markov game, MG)问题[108],实验场景例如囚徒困境问题和硬币博弈等.在MG问题中,如果各个智能体通过合作来最大化共同的回报,将其称为团队马尔科夫博弈[109](team Markov game, Team MG). ...
State of the Art-A Survey of Partially Observable Markov Decision Processes: Theory, Models, and Algorithms
1
1982
... 假如智能体的观测是局部的,对于利用个人目标实现集体回报最大化的,称为离散部分可观马尔科夫过程[110](decentralized partially observable Markov decision process, Dec-POMDP),其他的博弈称为部分可观马尔科夫过程(POMDP).棋牌类游戏常见的是序贯决策,当一方结束行动后,另一方开始行动,能够建模成扩展式博弈(extensive form games, EG)问题[111].此外,按照状态、动作的表示也分为连续空间和离散空间.处理不同空间数量级的问题,适用的算法也相应不同. ...
1
1953
... 假如智能体的观测是局部的,对于利用个人目标实现集体回报最大化的,称为离散部分可观马尔科夫过程[110](decentralized partially observable Markov decision process, Dec-POMDP),其他的博弈称为部分可观马尔科夫过程(POMDP).棋牌类游戏常见的是序贯决策,当一方结束行动后,另一方开始行动,能够建模成扩展式博弈(extensive form games, EG)问题[111].此外,按照状态、动作的表示也分为连续空间和离散空间.处理不同空间数量级的问题,适用的算法也相应不同. ...
Variational Autoencoders for Opponent Modeling in Multi-agent Systems
2
2001
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
... 非平稳性是指对手策略、环境状态转移、环境奖励不断发生变化,从而打破了MDP环境的马尔科夫性质,使得智能体无法学习到稳定的最优策略[117].诸如部分可观测、环境动态变化、对手策略学习等因素都会导致智能体的学习环境非平稳.因此,非平稳性智能体需要权衡模型学习潜在误差所导致的不确定性和在不确定性下的对手模型利用.例如,智能体无法获取对手当前的状态和动作信息,只能利用自身局部信息进行推理.为此,研究者通过无监督学习[118-119]从自身观测中提取被建模者的历史轨迹特征,建立对手模型.Papoudakis等[112-113]基于局部信息建模,采用变分自编码器(variational autoencoders, VAEs)学习历史轨迹的策略表征,并将其用于A3C算法的决策过程.然而,在智能体共同学习、智能种群演化等复杂动态问题中[43],策略难以收敛到静态最优,智能体陷入不断学习的循环.解决这类复杂任务中的非平稳性也是DRL-OM方法尚未解决的难题. ...
Agent Modelling under Partial Observability for Deep Reinforcement Learning
1
2021
... 非平稳性是指对手策略、环境状态转移、环境奖励不断发生变化,从而打破了MDP环境的马尔科夫性质,使得智能体无法学习到稳定的最优策略[117].诸如部分可观测、环境动态变化、对手策略学习等因素都会导致智能体的学习环境非平稳.因此,非平稳性智能体需要权衡模型学习潜在误差所导致的不确定性和在不确定性下的对手模型利用.例如,智能体无法获取对手当前的状态和动作信息,只能利用自身局部信息进行推理.为此,研究者通过无监督学习[118-119]从自身观测中提取被建模者的历史轨迹特征,建立对手模型.Papoudakis等[112-113]基于局部信息建模,采用变分自编码器(variational autoencoders, VAEs)学习历史轨迹的策略表征,并将其用于A3C算法的决策过程.然而,在智能体共同学习、智能种群演化等复杂动态问题中[43],策略难以收敛到静态最优,智能体陷入不断学习的循环.解决这类复杂任务中的非平稳性也是DRL-OM方法尚未解决的难题. ...
Learning to Model Opponent Learning
2
2020
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
... 针对异构和不同机器学习方法的智能体,研究人员提出几种适应方法.Davies等[114]提出学习模仿对手模型(learning to model opponent learning, LeMOL),利用双向长短时记忆网络存储情节记忆,并模仿对手的学习过程.此外,Kim等[145]考虑单个智能体的轨迹影响对手学习过程的情况,提供了可解释的异构智能体学习框架. ...
Robust Opponent Modeling via Adversarial Ensemble Reinforcement Learning
3
2021
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
... 针对单个网络模型对策略表示能力不足的问题,Shen等[115]在学习对手策略时采用集成学习方法[139]训练多个网络共同表示当前对手模型,提高了模型的鲁棒性.除了集成学习思想,知识蒸馏也是提高模型准确性的一种方法[140].知识蒸馏综合了多种专家网络,压缩网络结构信息,保留学习到的知识,经过知识蒸馏后的对手策略模型仍然保留了网络的对手特征提取能力[68,115]. ...
... ,115]. ...
Benchmarking Model-based Reinforcement Learning
1
1907
... Common experimental scenarios, game models, literature sources and problem characteristics
Table 5| 实验环境 | 博弈模型 | 文献 | 可观测信息 | 合作关系 | 行动顺序 | 状态动作 |
|---|
| 粒子世界 | POMDP | [56-57,112-114] | 部分可观 | 混合 | 同步 | 连续 |
| 德州扑克 | EG | [38,40-42] | 全局可观 | 竞争 | 序贯 | 离散 |
| 囚徒/硬币博弈 | MG | [80] | 全局可观 | 竞争 | 同步 | 离散 |
| 多智能体Mujoco | POMDP | [115] | 部分可观 | 混合 | 同步 | 连续 |
| 网格世界 | MG | [66-69] | 全局可观 | 混合 | 同步 | 连续 |
| 迭代矩阵游戏 | Team MG | [64,78] | 全局可观 | 竞争 | 同步 | 离散 |
| 智力竞赛碗 | EG | [26,71] | 全局可观 | 竞争 | 序贯 | 离散 |
| 炸弹人 | MG | [72] | 全局可观 | 竞争 | 同步 | 离散 |
| 合作导航 | Dec-POMDP | [63-64,116] | 部分可观 | 合作 | 同步 | 离散 |
| FightingICE | MG | [84,107] | 全局可观 | 竞争 | 同步 | 连续 |
| 谷歌足球环境 | POMDP | [87] | 部分可观 | 混合 | 同步 | 连续 |
5 关键问题与发展方向当前DRL-OM方法普遍面临着决策实时性差、难以应对非平稳性、模型学习效率低、无法有效地识别和使用欺骗以及对手利用等热点问题,为了在现实应用中更好地发挥作用,未来该领域可以从有模型强化学习、对手建模算法鲁棒性、对手快速适应性等方向开展研究.对此,本节针对关键问题和发展方向分别展开分析与探讨. ...
Dealing with Non-stationarity in Multi-agent Deep Reinforcement Learning
1
1906
... 非平稳性是指对手策略、环境状态转移、环境奖励不断发生变化,从而打破了MDP环境的马尔科夫性质,使得智能体无法学习到稳定的最优策略[117].诸如部分可观测、环境动态变化、对手策略学习等因素都会导致智能体的学习环境非平稳.因此,非平稳性智能体需要权衡模型学习潜在误差所导致的不确定性和在不确定性下的对手模型利用.例如,智能体无法获取对手当前的状态和动作信息,只能利用自身局部信息进行推理.为此,研究者通过无监督学习[118-119]从自身观测中提取被建模者的历史轨迹特征,建立对手模型.Papoudakis等[112-113]基于局部信息建模,采用变分自编码器(variational autoencoders, VAEs)学习历史轨迹的策略表征,并将其用于A3C算法的决策过程.然而,在智能体共同学习、智能种群演化等复杂动态问题中[43],策略难以收敛到静态最优,智能体陷入不断学习的循环.解决这类复杂任务中的非平稳性也是DRL-OM方法尚未解决的难题. ...
The Autoencoding Variational Autoencoder
1
2020
... 非平稳性是指对手策略、环境状态转移、环境奖励不断发生变化,从而打破了MDP环境的马尔科夫性质,使得智能体无法学习到稳定的最优策略[117].诸如部分可观测、环境动态变化、对手策略学习等因素都会导致智能体的学习环境非平稳.因此,非平稳性智能体需要权衡模型学习潜在误差所导致的不确定性和在不确定性下的对手模型利用.例如,智能体无法获取对手当前的状态和动作信息,只能利用自身局部信息进行推理.为此,研究者通过无监督学习[118-119]从自身观测中提取被建模者的历史轨迹特征,建立对手模型.Papoudakis等[112-113]基于局部信息建模,采用变分自编码器(variational autoencoders, VAEs)学习历史轨迹的策略表征,并将其用于A3C算法的决策过程.然而,在智能体共同学习、智能种群演化等复杂动态问题中[43],策略难以收敛到静态最优,智能体陷入不断学习的循环.解决这类复杂任务中的非平稳性也是DRL-OM方法尚未解决的难题. ...
1
2001
... 非平稳性是指对手策略、环境状态转移、环境奖励不断发生变化,从而打破了MDP环境的马尔科夫性质,使得智能体无法学习到稳定的最优策略[117].诸如部分可观测、环境动态变化、对手策略学习等因素都会导致智能体的学习环境非平稳.因此,非平稳性智能体需要权衡模型学习潜在误差所导致的不确定性和在不确定性下的对手模型利用.例如,智能体无法获取对手当前的状态和动作信息,只能利用自身局部信息进行推理.为此,研究者通过无监督学习[118-119]从自身观测中提取被建模者的历史轨迹特征,建立对手模型.Papoudakis等[112-113]基于局部信息建模,采用变分自编码器(variational autoencoders, VAEs)学习历史轨迹的策略表征,并将其用于A3C算法的决策过程.然而,在智能体共同学习、智能种群演化等复杂动态问题中[43],策略难以收敛到静态最优,智能体陷入不断学习的循环.解决这类复杂任务中的非平稳性也是DRL-OM方法尚未解决的难题. ...
Zero-shot Reinforcement Learning with Deep Attention Convolutional Neural Networks
1
2001
... 如何快速准确地训练对手模型,提升数据利用率是对手建模的关键问题.一方面,DRL-OM方法需要巨大的训练量和准确的奖励值作为指导,现实世界中的任务无法满足上述条件,因此,限制了应用场景[120-121];另一方面,具有自适应能力的对手策略导致模型不断变化,交互数据具有时效性,快速适应对手动态变化是解决方法之一[122].因此,如何避免学习过程消耗大量样本,从而以较少数据量在线学习到对手的策略是提升模型学习效率的关键问题. ...
Generalizing from a Few Eamples: A Survey on Few-shot Learning
1
2020
... 如何快速准确地训练对手模型,提升数据利用率是对手建模的关键问题.一方面,DRL-OM方法需要巨大的训练量和准确的奖励值作为指导,现实世界中的任务无法满足上述条件,因此,限制了应用场景[120-121];另一方面,具有自适应能力的对手策略导致模型不断变化,交互数据具有时效性,快速适应对手动态变化是解决方法之一[122].因此,如何避免学习过程消耗大量样本,从而以较少数据量在线学习到对手的策略是提升模型学习效率的关键问题. ...
Model-agnostic Meta-Learning for Fast Adaptation of Deep Networks
1
2017
... 如何快速准确地训练对手模型,提升数据利用率是对手建模的关键问题.一方面,DRL-OM方法需要巨大的训练量和准确的奖励值作为指导,现实世界中的任务无法满足上述条件,因此,限制了应用场景[120-121];另一方面,具有自适应能力的对手策略导致模型不断变化,交互数据具有时效性,快速适应对手动态变化是解决方法之一[122].因此,如何避免学习过程消耗大量样本,从而以较少数据量在线学习到对手的策略是提升模型学习效率的关键问题. ...
Bayes' Bluff: Opponent Modelling in Poker
1
2005
... 智能体如何使用欺骗策略和如何识别对手欺骗策略是对手建模研究的关键问题.在棋牌游戏中,智能体采用诈唬策略诱使对手放弃应有的收益[123].在即时策略类游戏中,通过“示弱”诱敌深入,放弃短期高收益的策略而采用伪装策略迷惑敌人[124],这些都是典型的欺骗策略.Bontrager等[125]分析了基于DRL的智能体在欺骗性游戏中的表现,实验结果表明对比规划类方法,DRL方法无法有效地应对环境中的欺骗.尽管对手建模的子领域意图识别提供了诸多识别欺骗的解决方案[126-127],但是当前的DRL-OM方法缺少对欺骗行为的研究,这一领域有很大的研究潜力. ...
Multiagent Bidirectionally-Coordinated Nets: Emergence of Human-level Coordination in Learning to Play Starcraft Combat Games
1
1703
... 智能体如何使用欺骗策略和如何识别对手欺骗策略是对手建模研究的关键问题.在棋牌游戏中,智能体采用诈唬策略诱使对手放弃应有的收益[123].在即时策略类游戏中,通过“示弱”诱敌深入,放弃短期高收益的策略而采用伪装策略迷惑敌人[124],这些都是典型的欺骗策略.Bontrager等[125]分析了基于DRL的智能体在欺骗性游戏中的表现,实验结果表明对比规划类方法,DRL方法无法有效地应对环境中的欺骗.尽管对手建模的子领域意图识别提供了诸多识别欺骗的解决方案[126-127],但是当前的DRL-OM方法缺少对欺骗行为的研究,这一领域有很大的研究潜力. ...
"Superstition" in the Network: Deep Reinforcement Learning Plays Deceptive Games
1
2019
... 智能体如何使用欺骗策略和如何识别对手欺骗策略是对手建模研究的关键问题.在棋牌游戏中,智能体采用诈唬策略诱使对手放弃应有的收益[123].在即时策略类游戏中,通过“示弱”诱敌深入,放弃短期高收益的策略而采用伪装策略迷惑敌人[124],这些都是典型的欺骗策略.Bontrager等[125]分析了基于DRL的智能体在欺骗性游戏中的表现,实验结果表明对比规划类方法,DRL方法无法有效地应对环境中的欺骗.尽管对手建模的子领域意图识别提供了诸多识别欺骗的解决方案[126-127],但是当前的DRL-OM方法缺少对欺骗行为的研究,这一领域有很大的研究潜力. ...
Fraud detection: Intentionality and Deception in Cognition
1
1993
... 智能体如何使用欺骗策略和如何识别对手欺骗策略是对手建模研究的关键问题.在棋牌游戏中,智能体采用诈唬策略诱使对手放弃应有的收益[123].在即时策略类游戏中,通过“示弱”诱敌深入,放弃短期高收益的策略而采用伪装策略迷惑敌人[124],这些都是典型的欺骗策略.Bontrager等[125]分析了基于DRL的智能体在欺骗性游戏中的表现,实验结果表明对比规划类方法,DRL方法无法有效地应对环境中的欺骗.尽管对手建模的子领域意图识别提供了诸多识别欺骗的解决方案[126-127],但是当前的DRL-OM方法缺少对欺骗行为的研究,这一领域有很大的研究潜力. ...
Extended Goal Recognition: A Planning-based Model for Strategic Deception
1
2021
... 智能体如何使用欺骗策略和如何识别对手欺骗策略是对手建模研究的关键问题.在棋牌游戏中,智能体采用诈唬策略诱使对手放弃应有的收益[123].在即时策略类游戏中,通过“示弱”诱敌深入,放弃短期高收益的策略而采用伪装策略迷惑敌人[124],这些都是典型的欺骗策略.Bontrager等[125]分析了基于DRL的智能体在欺骗性游戏中的表现,实验结果表明对比规划类方法,DRL方法无法有效地应对环境中的欺骗.尽管对手建模的子领域意图识别提供了诸多识别欺骗的解决方案[126-127],但是当前的DRL-OM方法缺少对欺骗行为的研究,这一领域有很大的研究潜力. ...
Balancing Safety and Exploitability in Opponent Modeling
1
2011
... 对手利用(opponent exploitation)指发现对手有限理性的弱点,并根据对手偏离绝对理性的行动制定收益更高的策略.衡量对手策略可利用度的方式是对手策略与纳什均衡策略期望收益之间的差值[128].Ganzfried等[129]提出博弈安全策略的表示形式,保证自身安全的同时利用对手的非最优策略,并在Kuhn扑克中超越学习纳什均衡策略的方法.DRL算法如何安全利用对手智能体,以及在更复杂场景计算对手利用策略,是DRL-OM领域值得探究的问题. ...
Safe Opponent Exploitation
1
2015
... 对手利用(opponent exploitation)指发现对手有限理性的弱点,并根据对手偏离绝对理性的行动制定收益更高的策略.衡量对手策略可利用度的方式是对手策略与纳什均衡策略期望收益之间的差值[128].Ganzfried等[129]提出博弈安全策略的表示形式,保证自身安全的同时利用对手的非最优策略,并在Kuhn扑克中超越学习纳什均衡策略的方法.DRL算法如何安全利用对手智能体,以及在更复杂场景计算对手利用策略,是DRL-OM领域值得探究的问题. ...
PILCO: A Model-based and Data-efficient Approach to Policy Search
1
2011
... 在现有的对手建模方法中,自身智能体将其余智能体连同环境一起看作整体建模,忽视了对手模型在外部环境中的演化过程,无法有效地推理对手的行为.研究者们希望借助有模型强化学习显式地建立环境动力学模型[130-132],将对手和环境之间的耦合进行拆解,帮助智能体更好地进行推理. ...
Deep Reinforcement Learning in a Handful of Trials Using Probabilistic Dynamics Models
0
2018
Model-based Multi-agent Policy Optimization with Adaptive Opponent-wise Rollouts
2
2105
... 在现有的对手建模方法中,自身智能体将其余智能体连同环境一起看作整体建模,忽视了对手模型在外部环境中的演化过程,无法有效地推理对手的行为.研究者们希望借助有模型强化学习显式地建立环境动力学模型[130-132],将对手和环境之间的耦合进行拆解,帮助智能体更好地进行推理. ...
... 为此,Yu等[87]提出一种基于环境模型的贝叶斯递归推理方法,通过贝叶斯定理分配对手采取每种策略的权重,并将不同递归层次的策略组合构成对手策略,该算法在保证效率的同时避免了获取对手先验知识.Zhang等[132]将有模型强化学习的模型误差分为环境动态误差和对手模型误差,开发了自适应调整采样长度的对手建模误差控制方法,使用虚拟的对手和环境模型自演交互以扩充样本数据,达到高效利用数据的目的. ...
Risk Averse Robust Adversarial Reinforcement Learning
1
2019
... DRL-OM方法通常需要智能体与对手进行长时间的交互训练,由于采样存在不稳定性,策略更新容易发生策略遗忘和崩塌的情况[133].算法鲁棒性研究的是深度学习算法与环境进行交互时,如何保证策略不受限于局部最优以及策略不因采样误差而在更新中变差的问题[134-136].除此之外,仿真环境与现实系统出现不匹配时,对手建模算法的鲁棒性决定了能否在模型迁移后保证其实用性[137-138]. ...
Robust Reinforcement Learning Using Adversarial Populations
1
2008
... DRL-OM方法通常需要智能体与对手进行长时间的交互训练,由于采样存在不稳定性,策略更新容易发生策略遗忘和崩塌的情况[133].算法鲁棒性研究的是深度学习算法与环境进行交互时,如何保证策略不受限于局部最优以及策略不因采样误差而在更新中变差的问题[134-136].除此之外,仿真环境与现实系统出现不匹配时,对手建模算法的鲁棒性决定了能否在模型迁移后保证其实用性[137-138]. ...
Robust Learning with Missing Data
0
2001
1
2018
... DRL-OM方法通常需要智能体与对手进行长时间的交互训练,由于采样存在不稳定性,策略更新容易发生策略遗忘和崩塌的情况[133].算法鲁棒性研究的是深度学习算法与环境进行交互时,如何保证策略不受限于局部最优以及策略不因采样误差而在更新中变差的问题[134-136].除此之外,仿真环境与现实系统出现不匹配时,对手建模算法的鲁棒性决定了能否在模型迁移后保证其实用性[137-138]. ...
Robust Adversarial Reinforcement Learning
1
2017
... DRL-OM方法通常需要智能体与对手进行长时间的交互训练,由于采样存在不稳定性,策略更新容易发生策略遗忘和崩塌的情况[133].算法鲁棒性研究的是深度学习算法与环境进行交互时,如何保证策略不受限于局部最优以及策略不因采样误差而在更新中变差的问题[134-136].除此之外,仿真环境与现实系统出现不匹配时,对手建模算法的鲁棒性决定了能否在模型迁移后保证其实用性[137-138]. ...
Extending Robust Adversarial Reinforcement Learning Considering Adaptation and Diversity
1
1703
... DRL-OM方法通常需要智能体与对手进行长时间的交互训练,由于采样存在不稳定性,策略更新容易发生策略遗忘和崩塌的情况[133].算法鲁棒性研究的是深度学习算法与环境进行交互时,如何保证策略不受限于局部最优以及策略不因采样误差而在更新中变差的问题[134-136].除此之外,仿真环境与现实系统出现不匹配时,对手建模算法的鲁棒性决定了能否在模型迁移后保证其实用性[137-138]. ...
Ensemble Learning: A Survey
1
8
... 针对单个网络模型对策略表示能力不足的问题,Shen等[115]在学习对手策略时采用集成学习方法[139]训练多个网络共同表示当前对手模型,提高了模型的鲁棒性.除了集成学习思想,知识蒸馏也是提高模型准确性的一种方法[140].知识蒸馏综合了多种专家网络,压缩网络结构信息,保留学习到的知识,经过知识蒸馏后的对手策略模型仍然保留了网络的对手特征提取能力[68,115]. ...
Distilling the Knowledge in a Neural Network
1
1503
... 针对单个网络模型对策略表示能力不足的问题,Shen等[115]在学习对手策略时采用集成学习方法[139]训练多个网络共同表示当前对手模型,提高了模型的鲁棒性.除了集成学习思想,知识蒸馏也是提高模型准确性的一种方法[140].知识蒸馏综合了多种专家网络,压缩网络结构信息,保留学习到的知识,经过知识蒸馏后的对手策略模型仍然保留了网络的对手特征提取能力[68,115]. ...
Prefrontal Cortex as a Meta-reinforcement Learning System
1
2018
... 对手建模面临着难以适应具有学习能力的对手以及对新出现对手的重新适应等问题,元学习是实现智能体快速学习的途径[141-144].一方面,它通过掌握已有的经验知识来指导新的任务,解决了重新训练和奖励函数构造的难题;另一方面,针对复杂动作空间的对手建模,元学习提供更高层次的策略控制.例如,Kim等[145]提出一种多智能体元策略梯度方法,将多智能体博弈过程建立为一种联合策略马尔科夫链,使用梯度优化主体智能体的初始参数,同时链式更新对其他智能体,达到快速适应对手的目的. ...
Learning to Adapt in Dynamic, Real-world Environments through Meta-reinforcement Learning
0
1803
Meta-world: A Benchmark and Evaluation for Multi-task and Meta Reinforcement Learning
0
2020
Meta-reinforcement Learning of Structured Exploration Strategies
1
2018
... 对手建模面临着难以适应具有学习能力的对手以及对新出现对手的重新适应等问题,元学习是实现智能体快速学习的途径[141-144].一方面,它通过掌握已有的经验知识来指导新的任务,解决了重新训练和奖励函数构造的难题;另一方面,针对复杂动作空间的对手建模,元学习提供更高层次的策略控制.例如,Kim等[145]提出一种多智能体元策略梯度方法,将多智能体博弈过程建立为一种联合策略马尔科夫链,使用梯度优化主体智能体的初始参数,同时链式更新对其他智能体,达到快速适应对手的目的. ...
A Policy Gradient Algorithm for Learning to Learn in Multiagent Reinforcement Learning
2
2021
... 对手建模面临着难以适应具有学习能力的对手以及对新出现对手的重新适应等问题,元学习是实现智能体快速学习的途径[141-144].一方面,它通过掌握已有的经验知识来指导新的任务,解决了重新训练和奖励函数构造的难题;另一方面,针对复杂动作空间的对手建模,元学习提供更高层次的策略控制.例如,Kim等[145]提出一种多智能体元策略梯度方法,将多智能体博弈过程建立为一种联合策略马尔科夫链,使用梯度优化主体智能体的初始参数,同时链式更新对其他智能体,达到快速适应对手的目的. ...
... 针对异构和不同机器学习方法的智能体,研究人员提出几种适应方法.Davies等[114]提出学习模仿对手模型(learning to model opponent learning, LeMOL),利用双向长短时记忆网络存储情节记忆,并模仿对手的学习过程.此外,Kim等[145]考虑单个智能体的轨迹影响对手学习过程的情况,提供了可解释的异构智能体学习框架. ...